Daniel Sousa
Joint Characterization of the Cryospheric Spectral Feature Space
Dec 02, 2021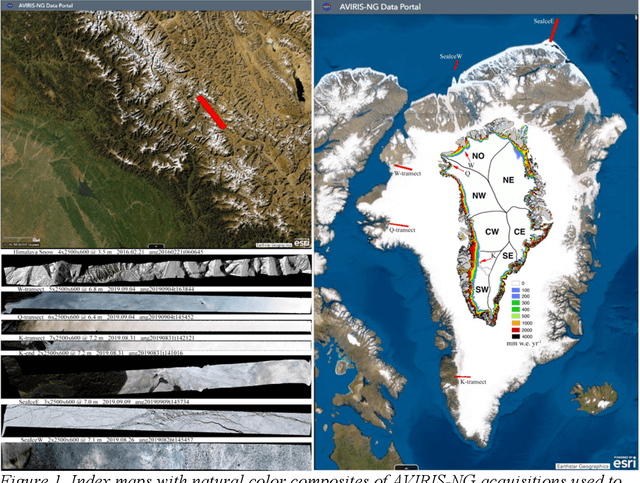
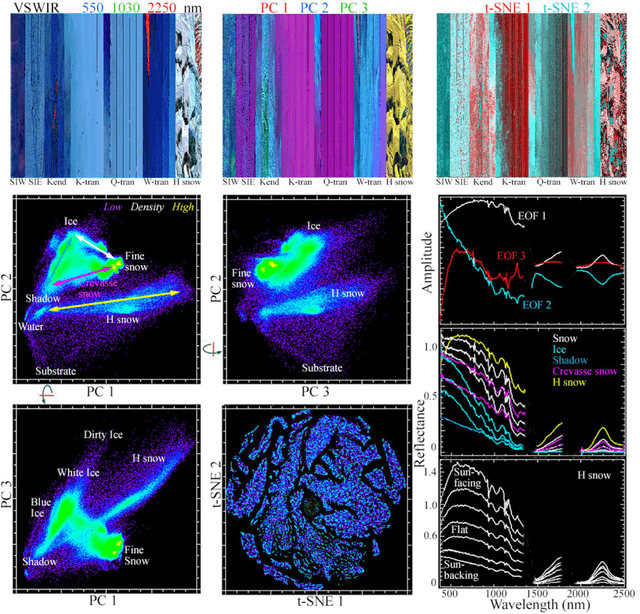
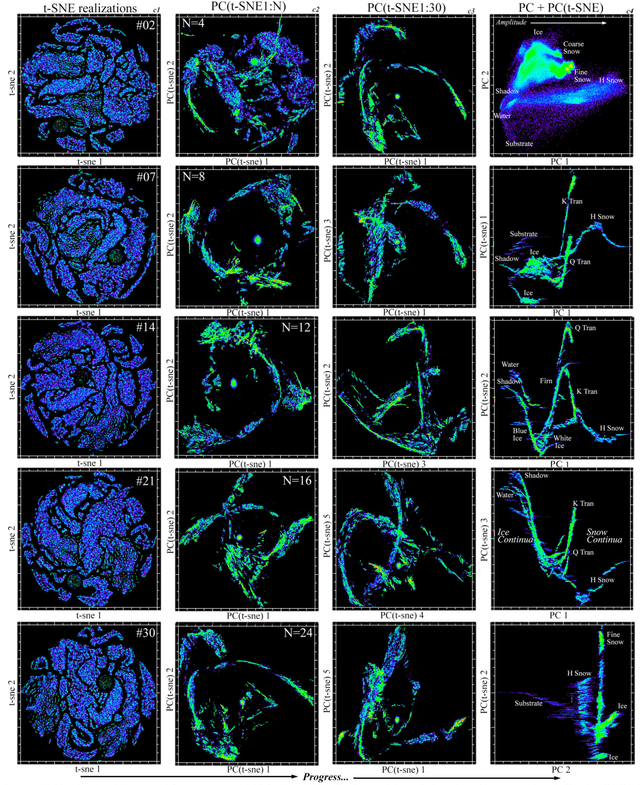
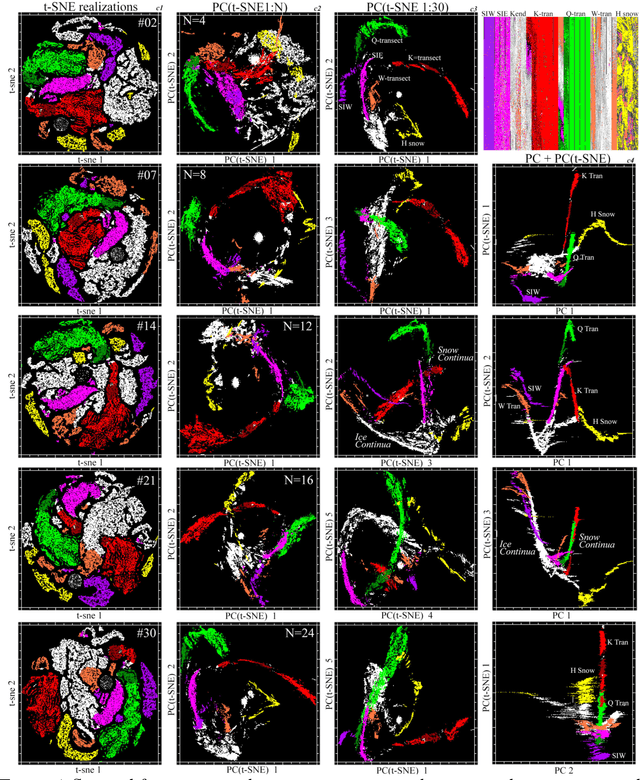
Abstract:Hyperspectral feature spaces are useful for many remote sensing applications ranging from spectral mixture modeling to discrete thematic classification. In such cases, characterization of the feature space dimensionality, geometry and topology can provide guidance for effective model design. The objective of this study is to compare and contrast two approaches for identifying feature space basis vectors via dimensionality reduction. These approaches can be combined to render a joint characterization that reveals spectral properties not apparent using either approach alone. We use a diverse collection of AVIRIS-NG reflectance spectra of the snow-firn-ice continuum to illustrate the utility of joint characterization and identify physical properties inferred from the spectra. Spectral feature spaces combining principal components (PCs) and t-distributed Stochastic Neighbor Embeddings (t-SNEs) provide physically interpretable dimensions representing the global (PC) structure of cryospheric reflectance properties and local (t-SNE) manifold structures revealing clustering not resolved in the global continuum. Joint characterization reveals distinct continua for snow-firn gradients on different parts of the Greenland Ice Sheet and multiple clusters of ice reflectance properties common to both glacier and sea ice in different locations. Clustering revealed in t-SNE feature spaces, and extended to the joint characterization, distinguishes differences in spectral curvature specific to location within the snow accumulation zone, and BRDF effects related to view geometry. The ability of PC+t-SNE joint characterization to produce a physically interpretable spectral feature spaces revealing global topology while preserving local manifold structures suggests that this characterization might be extended to the much higher dimensional hyperspectral feature space of all terrestrial land cover.
Joint Characterization of Spatiotemporal Data Manifolds
Aug 21, 2021Abstract:Spatiotemporal (ST) image data are increasingly common and often high-dimensional (high-D). Modeling ST data can be a challenge due to the plethora of independent and interacting processes which may or may not contribute to the measurements. Characterization can be considered the complement to modeling by helping guide assumptions about generative processes and their representation in the data. Dimensionality reduction (DR) is a frequently implemented type of characterization designed to mitigate the "curse of dimensionality" on high-D signals. For decades, Principal Component (PC) and Empirical Orthogonal Function (EOF) analysis has been used as a linear, invertible approach to DR and ST analysis. Recent years have seen the additional development of a suite of nonlinear DR algorithms, frequently categorized as "manifold learning". Here, we explore the idea of joint characterization of ST data manifolds using PCs/EOFs alongside two nonlinear DR approaches: Laplacian Eigenmaps (LE) and t-distributed stochastic neighbor embedding (t-SNE). Starting with a synthetic example and progressing to global, regional, and field scale ST datasets spanning roughly 5 orders of magnitude in space and 2 in time, we show these three DR approaches can yield complementary information about ST manifold topology. Compared to the relatively diffuse TFS produced by PCs/EOFs, the nonlinear approaches yield more compact manifolds with decreased ambiguity in temporal endmembers (LE) and/or in spatiotemporal clustering (t-SNE). These properties are compensated by the greater interpretability, significantly lower computational demand and diminished sensitivity to spatial aliasing for PCs/EOFs than LE or t-SNE. Taken together, we find joint characterization using the three complementary DR approaches capable of greater insight into generative ST processes than possible using any single approach alone.
Joint Characterization of Multiscale Information in High Dimensional Data
Feb 18, 2021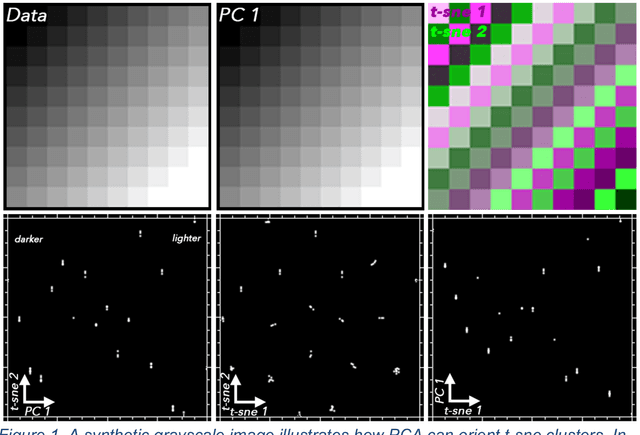
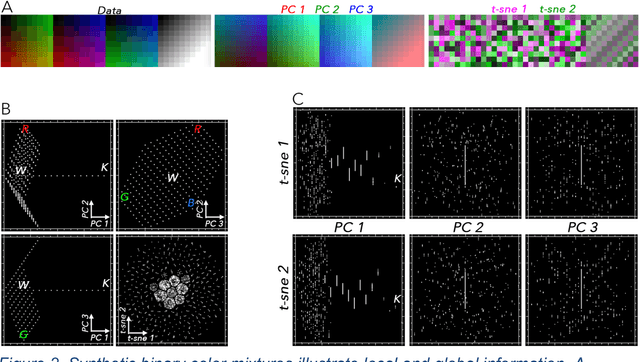
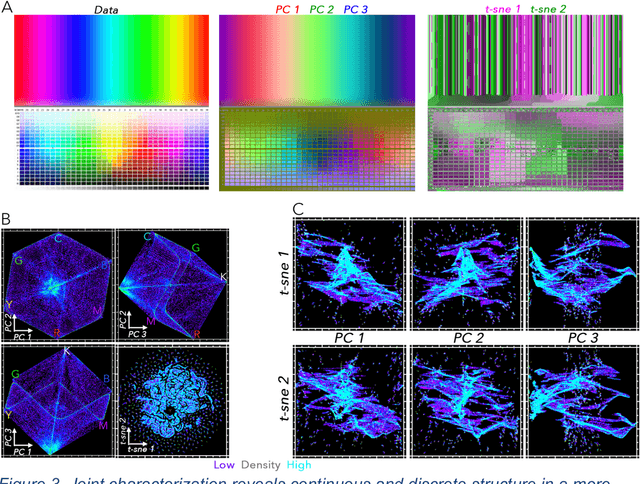
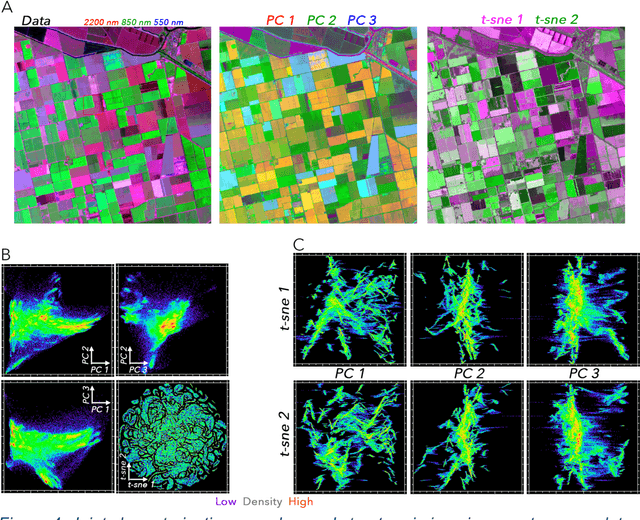
Abstract:High dimensional data can contain multiple scales of variance. Analysis tools that preferentially operate at one scale can be ineffective at capturing all the information present in this cross-scale complexity. We propose a multiscale joint characterization approach designed to exploit synergies between global and local approaches to dimensionality reduction. We illustrate this approach using Principal Components Analysis (PCA) to characterize global variance structure and t-stochastic neighbor embedding (t-sne) to characterize local variance structure. Using both synthetic images and real-world imaging spectroscopy data, we show that joint characterization is capable of detecting and isolating signals which are not evident from either PCA or t-sne alone. Broadly, t-sne is effective at rendering a randomly oriented low-dimensional map of local clusters, and PCA renders this map interpretable by providing global, physically meaningful structure. This approach is illustrated using imaging spectroscopy data, and may prove particularly useful for other geospatial data given robust local variance structure due to spatial autocorrelation and physical interpretability of global variance structure due to spectral properties of Earth surface materials. However, the fundamental premise could easily be extended to other high dimensional datasets, including image time series and non-image data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge