Sparse Portfolio Selection via Topological Data Analysis based Clustering

This paper uses topological data analysis (TDA) tools and introduces a data-driven clustering-based stock selection strategy tailored for sparse portfolio construction. Our asset selection strategy exploits the topological features of stock price movements to select a subset of topologically similar (different) assets for a sparse index tracking (Markowitz) portfolio. We introduce new distance measures, which serve as an input to the clustering algorithm, on the space of persistence diagrams and landscapes that consider the time component of a time series. We conduct an empirical analysis on the S\&P index from 2009 to 2020, including a study on the COVID-19 data to validate the robustness of our methodology. Our strategy to integrate TDA with the clustering algorithm significantly enhanced the performance of sparse portfolios across various performance measures in diverse market scenarios.

Empirical Asset Pricing via Ensemble Gaussian Process Regression

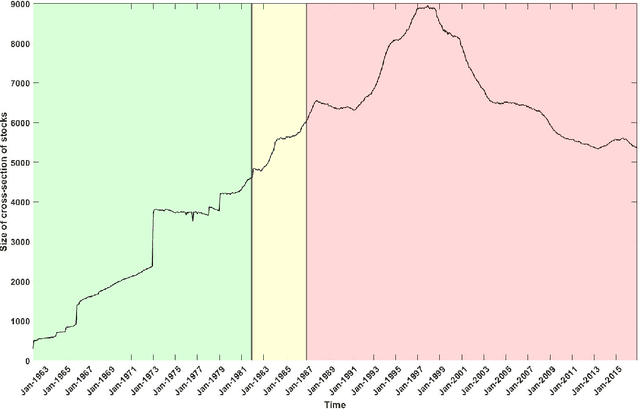
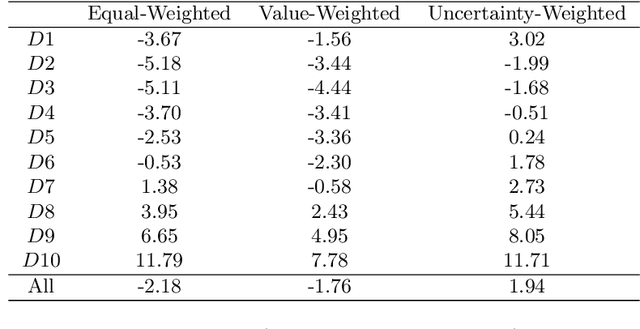
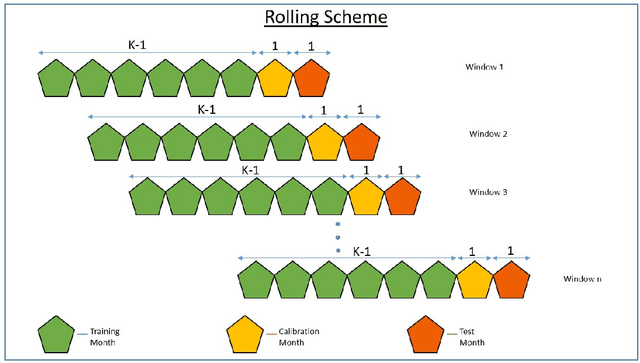
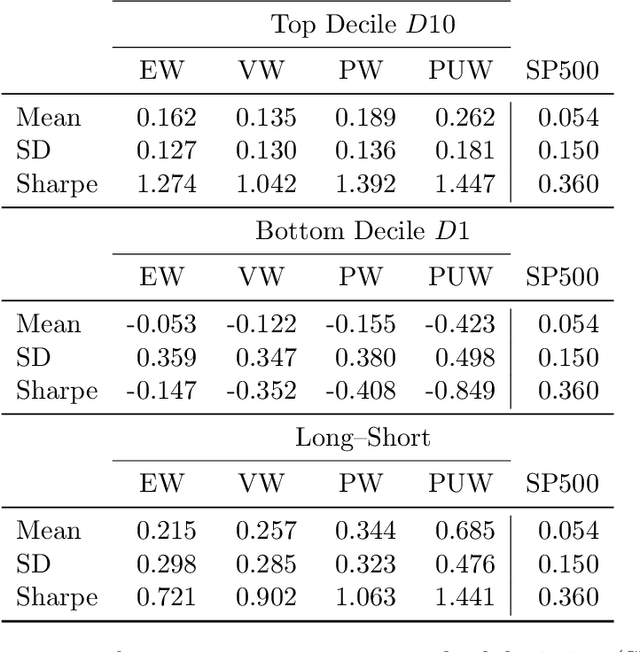
We introduce an ensemble learning method based on Gaussian Process Regression (GPR) for predicting conditional expected stock returns given stock-level and macro-economic information. Our ensemble learning approach significantly reduces the computational complexity inherent in GPR inference and lends itself to general online learning tasks. We conduct an empirical analysis on a large cross-section of US stocks from 1962 to 2016. We find that our method dominates existing machine learning models statistically and economically in terms of out-of-sample $R$-squared and Sharpe ratio of prediction-sorted portfolios. Exploiting the Bayesian nature of GPR, we introduce the mean-variance optimal portfolio with respect to the predictive uncertainty distribution of the expected stock returns. It appeals to an uncertainty averse investor and significantly dominates the equal- and value-weighted prediction-sorted portfolios, which outperform the S&P 500.