Scalable k-Means Clustering for Large k via Seeded Approximate Nearest-Neighbor Search

For very large values of $k$, we consider methods for fast $k$-means clustering of massive datasets with $10^7\sim10^9$ points in high-dimensions ($d\geq100$). All current practical methods for this problem have runtimes at least $\Omega(k^2)$. We find that initialization routines are not a bottleneck for this case. Instead, it is critical to improve the speed of Lloyd's local-search algorithm, particularly the step that reassigns points to their closest center. Attempting to improve this step naturally leads us to leverage approximate nearest-neighbor search methods, although this alone is not enough to be practical. Instead, we propose a family of problems we call "Seeded Approximate Nearest-Neighbor Search", for which we propose "Seeded Search-Graph" methods as a solution.

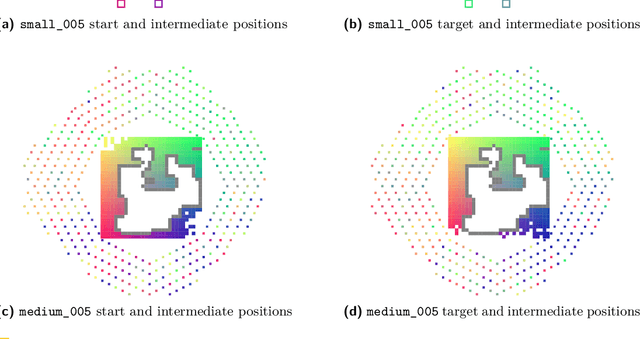
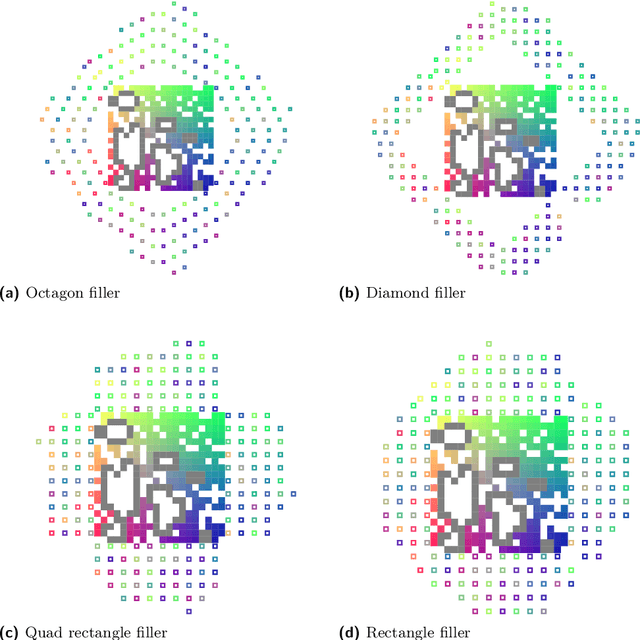
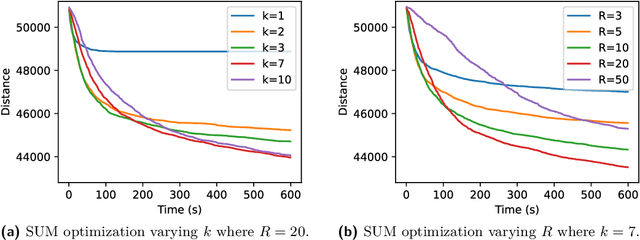
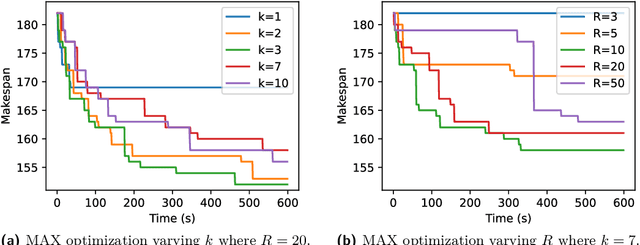
Coordinated Motion Planning Through Randomized k-Opt

This paper examines the approach taken by team gitastrophe in the CG:SHOP 2021 challenge. The challenge was to find a sequence of simultaneous moves of square robots between two given configurations that minimized either total distance travelled or makespan (total time). Our winning approach has two main components: an initialization phase that finds a good initial solution, and a $k$-opt local search phase which optimizes this solution. This led to a first place finish in the distance category and a third place finish in the makespan category.