Exact Inference for Relational Graphical Models with Interpreted Functions: Lifted Probabilistic Inference Modulo Theories

Probabilistic Inference Modulo Theories (PIMT) is a recent framework that expands exact inference on graphical models to use richer languages that include arithmetic, equalities, and inequalities on both integers and real numbers. In this paper, we expand PIMT to a lifted version that also processes random functions and relations. This enhancement is achieved by adapting Inversion, a method from Lifted First-Order Probabilistic Inference literature, to also be modulo theories. This results in the first algorithm for exact probabilistic inference that efficiently and simultaneously exploits random relations and functions, arithmetic, equalities and inequalities.

Probabilistic Inference Modulo Theories

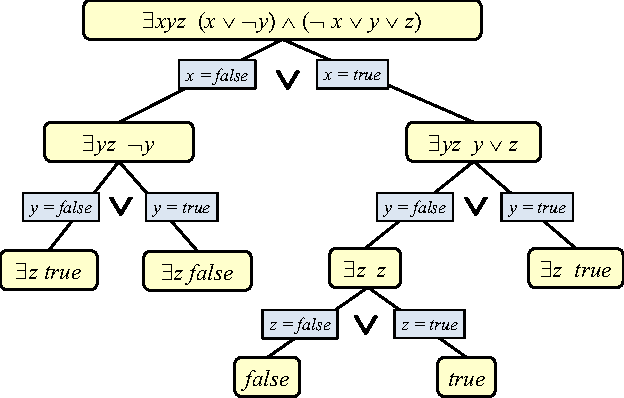
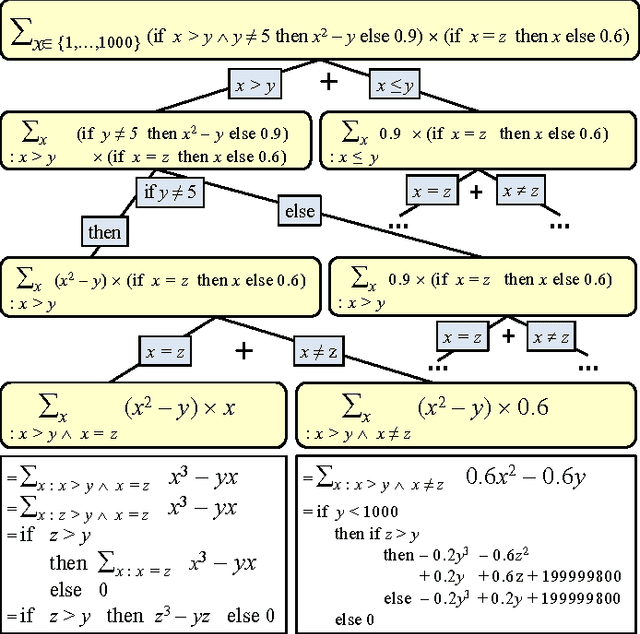
We present SGDPLL(T), an algorithm that solves (among many other problems) probabilistic inference modulo theories, that is, inference problems over probabilistic models defined via a logic theory provided as a parameter (currently, propositional, equalities on discrete sorts, and inequalities, more specifically difference arithmetic, on bounded integers). While many solutions to probabilistic inference over logic representations have been proposed, SGDPLL(T) is simultaneously (1) lifted, (2) exact and (3) modulo theories, that is, parameterized by a background logic theory. This offers a foundation for extending it to rich logic languages such as data structures and relational data. By lifted, we mean algorithms with constant complexity in the domain size (the number of values that variables can take). We also detail a solver for summations with difference arithmetic and show experimental results from a scenario in which SGDPLL(T) is much faster than a state-of-the-art probabilistic solver.