Active Manifolds: A non-linear analogue to Active Subspaces

We present an approach to analyze $C^1(\mathbb{R}^m)$ functions that addresses limitations present in the Active Subspaces (AS) method of Constantine et al.(2015; 2014). Under appropriate hypotheses, our Active Manifolds (AM) method identifies a 1-D curve in the domain (the active manifold) on which nearly all values of the unknown function are attained, and which can be exploited for approximation or analysis, especially when $m$ is large (high-dimensional input space). We provide theorems justifying our AM technique and an algorithm permitting functional approximation and sensitivity analysis. Using accessible, low-dimensional functions as initial examples, we show AM reduces approximation error by an order of magnitude compared to AS, at the expense of more computation. Following this, we revisit the sensitivity analysis by Glaws et al. (2017), who apply AS to analyze a magnetohydrodynamic power generator model, and compare the performance of AM on the same data. Our analysis provides detailed information not captured by AS, exhibiting the influence of each parameter individually along an active manifold. Overall, AM represents a novel technique for analyzing functional models with benefits including: reducing $m$-dimensional analysis to a 1-D analogue, permitting more accurate regression than AS (at more computational expense), enabling more informative sensitivity analysis, and granting accessible visualizations(2-D plots) of parameter sensitivity along the AM.

Dimension Reduction Using Active Manifolds

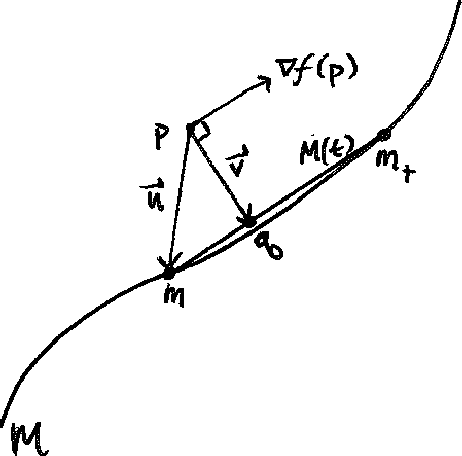
Scientists and engineers rely on accurate mathematical models to quantify the objects of their studies, which are often high-dimensional. Unfortunately, high-dimensional models are inherently difficult, i.e. when observations are sparse or expensive to determine. One way to address this problem is to approximate the original model with fewer input dimensions. Our project goal was to recover a function f that takes n inputs and returns one output, where n is potentially large. For any given n-tuple, we assume that we can observe a sample of the gradient and output of the function but it is computationally expensive to do so. This project was inspired by an approach known as Active Subspaces, which works by linearly projecting to a linear subspace where the function changes most on average. Our research gives mathematical developments informing a novel algorithm for this problem. Our approach, Active Manifolds, increases accuracy by seeking nonlinear analogues that approximate the function. The benefits of our approach are eliminated unprincipled parameter, choices, guaranteed accessible visualization, and improved estimation accuracy.