Rheumatoid Arthritis: Automated Scoring of Radiographic Joint Damage

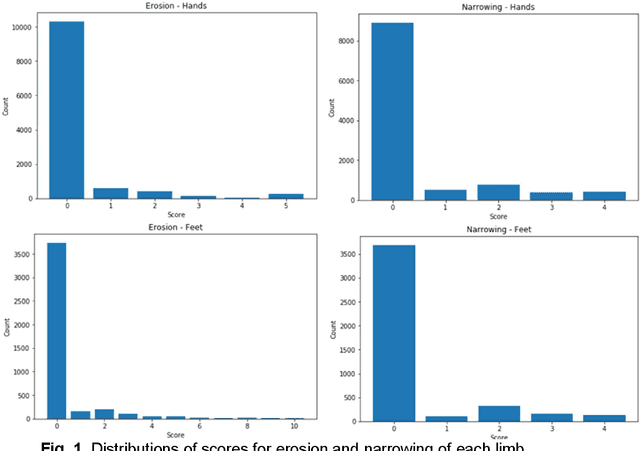
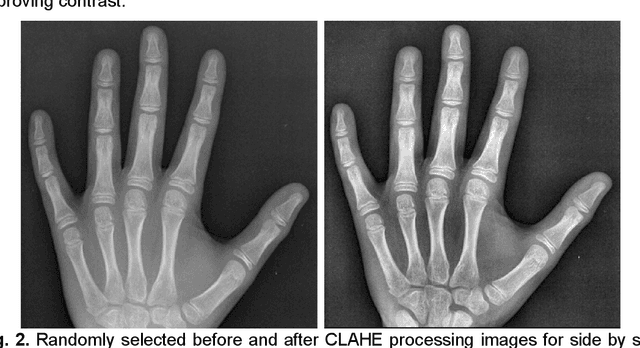
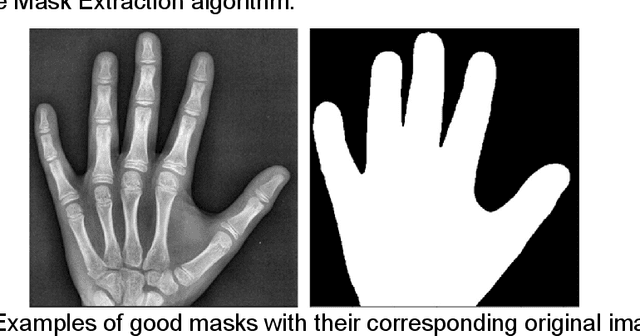
Rheumatoid arthritis is an autoimmune disease that causes joint damage due to inflammation in the soft tissue lining the joints known as the synovium. It is vital to identify joint damage as soon as possible to provide necessary treatment early and prevent further damage to the bone structures. Radiographs are often used to assess the extent of the joint damage. Currently, the scoring of joint damage from the radiograph takes expertise, effort, and time. Joint damage associated with rheumatoid arthritis is also not quantitated in clinical practice and subjective descriptors are used. In this work, we describe a pipeline of deep learning models to automatically identify and score rheumatoid arthritic joint damage from a radiographic image. Our automatic tool was shown to produce scores with extremely high balanced accuracy within a couple of minutes and utilizing this would remove the subjectivity of the scores between human reviewers.

Topological Machine Learning for Mixed Numeric and Categorical Data

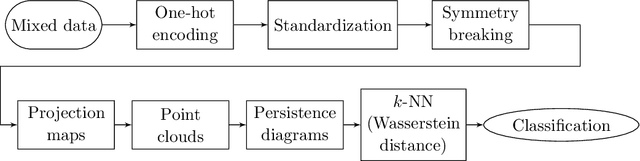
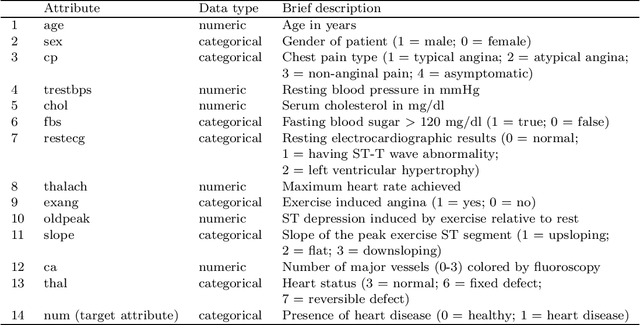
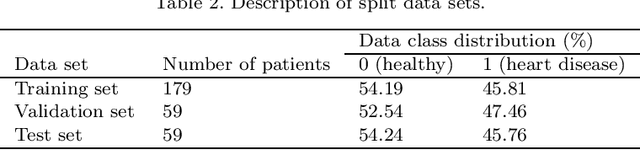
Topological data analysis is a relatively new branch of machine learning that excels in studying high dimensional data, and is theoretically known to be robust against noise. Meanwhile, data objects with mixed numeric and categorical attributes are ubiquitous in real-world applications. However, topological methods are usually applied to point cloud data, and to the best of our knowledge there is no available framework for the classification of mixed data using topological methods. In this paper, we propose a novel topological machine learning method for mixed data classification. In the proposed method, we use theory from topological data analysis such as persistent homology, persistence diagrams and Wasserstein distance to study mixed data. The performance of the proposed method is demonstrated by experiments on a real-world heart disease dataset. Experimental results show that our topological method outperforms several state-of-the-art algorithms in the prediction of heart disease.

Topological Machine Learning for Multivariate Time Series

We develop a framework for analyzing multivariate time series using topological data analysis (TDA) methods. The proposed methodology involves converting the multivariate time series to point cloud data, calculating Wasserstein distances between the persistence diagrams and using the $k$-nearest neighbors algorithm ($k$-NN) for supervised machine learning. Two methods (symmetry-breaking and anchor points) are also introduced to enable TDA to better analyze data with heterogeneous features that are sensitive to translation, rotation, or choice of coordinates. We apply our methods to room occupancy detection based on 5 time-dependent variables (temperature, humidity, light, CO2 and humidity ratio). Experimental results show that topological methods are effective in predicting room occupancy during a time window.