Avik Sarkar
Self-learning Emulators and Eigenvector Continuation
Jul 28, 2021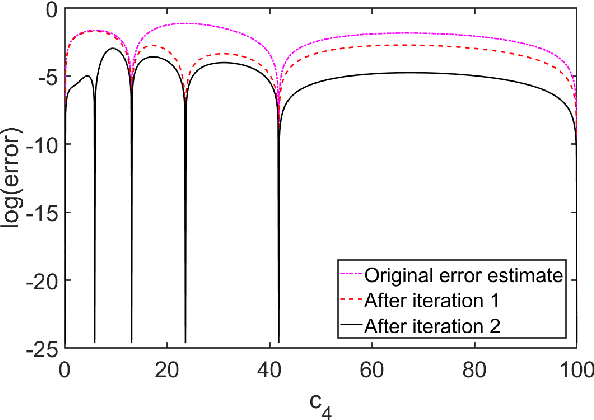
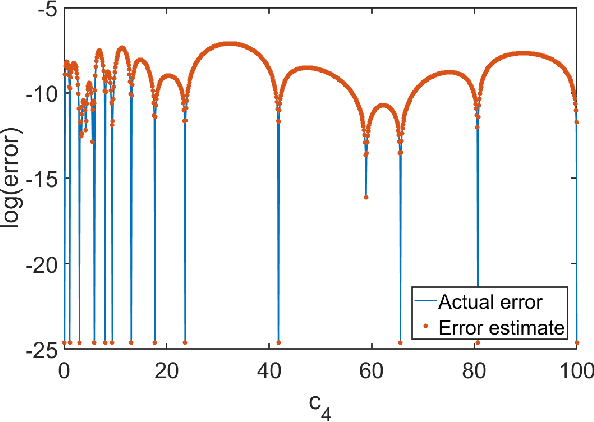
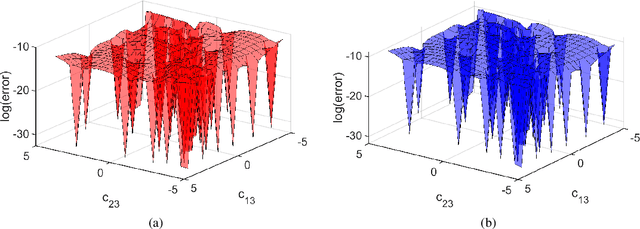
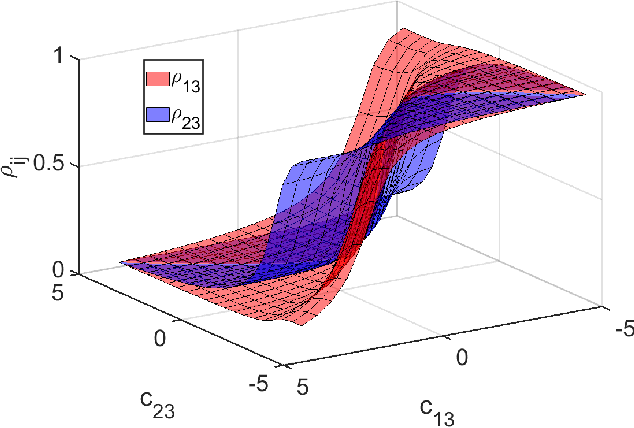
Abstract:Emulators that can bypass computationally expensive scientific calculations with high accuracy and speed can enable new studies of fundamental science as well as more potential applications. In this work we focus on solving a system of constraint equations efficiently using a new machine learning approach that we call self-learning emulation. A self-learning emulator is an active learning protocol that can rapidly solve a system of equations over some range of control parameters. The key ingredient is a fast estimate of the emulator error that becomes progressively more accurate as the emulator improves. This acceleration is possible because the emulator itself is used to estimate the error, and we illustrate with two examples. The first uses cubic spline interpolation to find the roots of a polynomial with variable coefficients. The second example uses eigenvector continuation to find the eigenvectors and eigenvalues of a large Hamiltonian matrix that depends on several control parameters. We envision future applications of self-learning emulators for solving systems of algebraic equations, linear and nonlinear differential equations, and linear and nonlinear eigenvalue problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge