TopoResNet: A hybrid deep learning architecture and its application to skin lesion classification

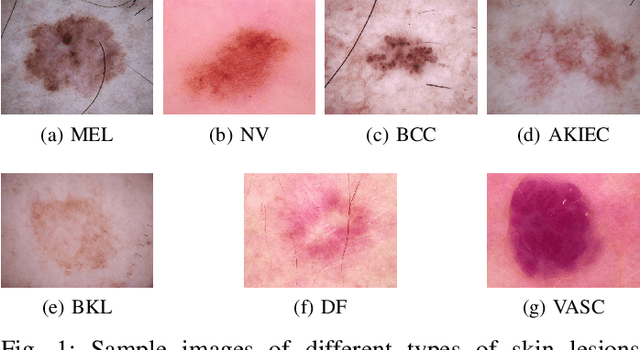
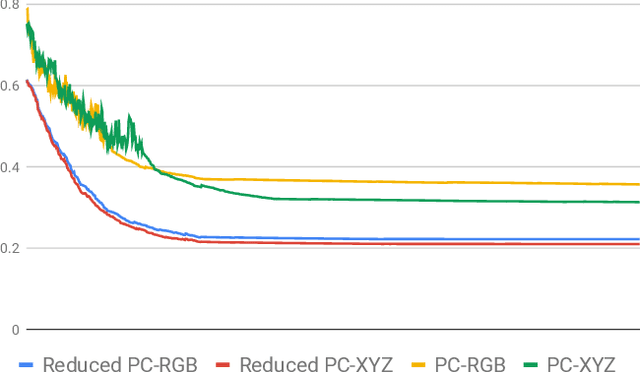
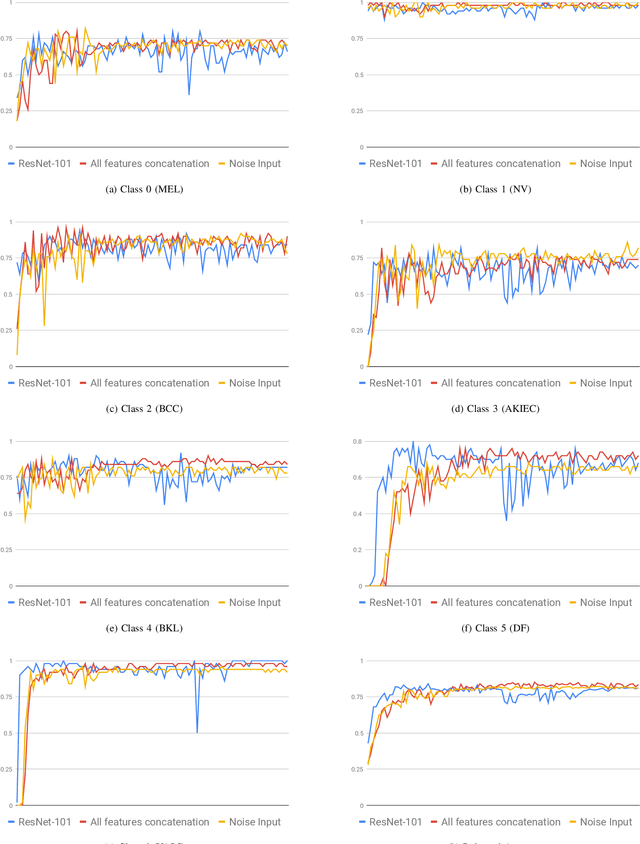
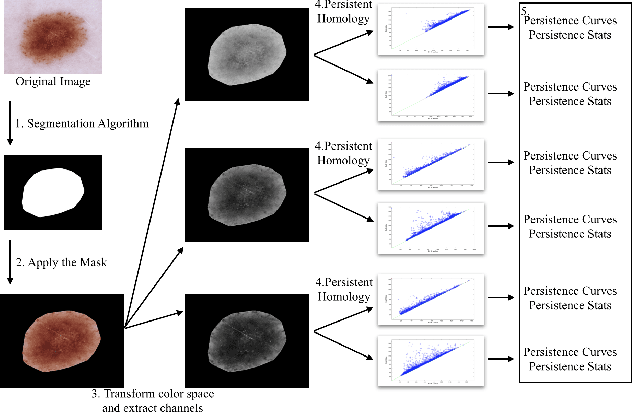
Skin cancer is one of the most common cancers in the United States. As technological advancements are made, algorithmic diagnosis of skin lesions is becoming more important. In this paper, we develop algorithms for segmenting the actual diseased area of skin in a given image of a skin lesion, and for classifying different types of skin lesions pictured in a given image. The cores of the algorithms used were based in persistent homology, an algebraic topology technique that is part of the rising field of Topological Data Analysis (TDA). The segmentation algorithm utilizes a similar concept to persistent homology that captures the robustness of segmented regions. For classification, we design two families of topological features from persistence diagrams---which we refer to as {\em persistence statistics} (PS) and {\em persistence curves} (PC), and use linear support vector machine as classifiers. We also combined those topological features, PS and PC, into ResNet-101 model, which we call {\em TopoResNet-101}, the results show that PS and PC are effective in two folds---improving classification performances and stabilizing the training process. Although convolutional features are the most important learning targets in CNN models, global information of images may be lost in the training process. Because topological features were extracted globally, our results show that the global property of topological features provide additional information to machine learning models.

Persistence Curves: A canonical framework for summarizing persistence diagrams

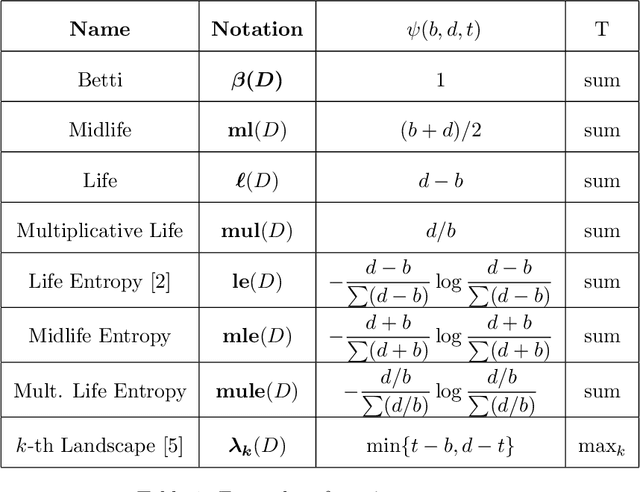
Persistence diagrams are a main tool in the field of Topological Data Analysis (TDA). They contain fruitful information about the shape of data. The use of machine learning algorithms on the space of persistence diagrams proves to be challenging as the space is complicated. For that reason, summarizing and vectorizing these diagrams is an important topic currently researched in TDA. In this work, we provide a general framework of summarizing diagrams that we call Persistence Curves (PC). The main idea is so-called Fundamental Lemma of Persistent Homology, which is derived from the classic elder rule. Under this framework, certain well-known summaries, such as persistent Betti numbers, and persistence landscape, are special cases of the PC. Moreover, we prove a rigorous bound for a general families of PCs. In particular, certain family of PCs admit the stability property under an additional assumption. Finally, we apply PCs to textures classification on four well-know texture datasets. The result outperforms several existing TDA methods.