Recovering low-rank structure from multiple networks with unknown edge distributions

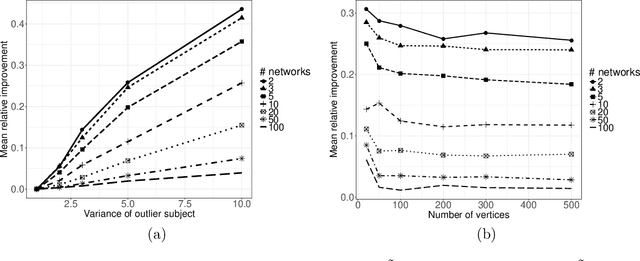
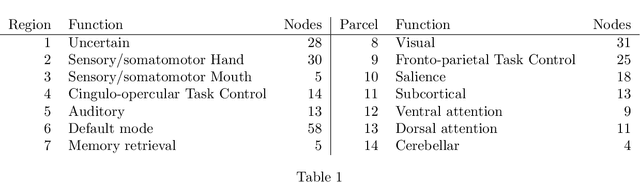
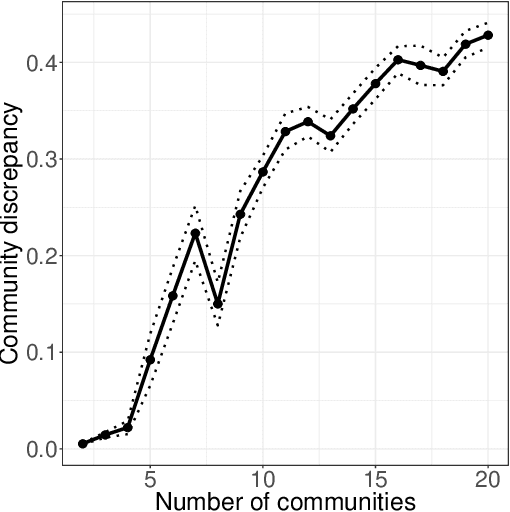
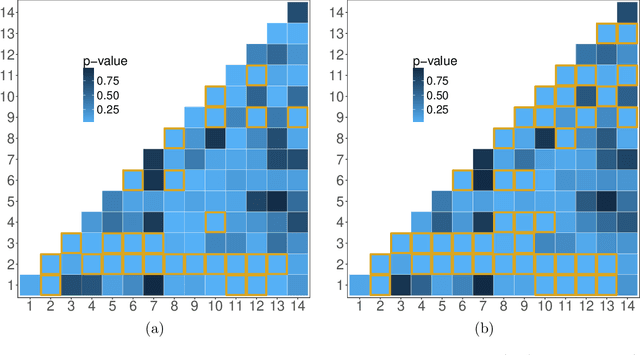
In increasingly many settings, particularly in neuroimaging, data sets consist of multiple samples from a population of networks, with vertices aligned across networks. For example, fMRI studies yield graphs whose vertices correspond to brain regions, which are the same across subjects. We consider the setting where we observe a sample of networks whose adjacency matrices have a shared low-rank expectation, but edge-level noise distributions may vary from one network to another. We show that so long as edge noise is sub-gamma distributed in each network, the shared low-rank structure can be recovered accurately using an eigenvalue truncation of a weighted network average. We also explore the extent to which edge-level errors influence estimation and downstream inference tasks. The proposed approach is illustrated on synthetic networks and on an fMRI study of schizophrenia.