Gradient flow on extensive-rank positive semi-definite matrix denoising

In this work, we present a new approach to analyze the gradient flow for a positive semi-definite matrix denoising problem in an extensive-rank and high-dimensional regime. We use recent linear pencil techniques of random matrix theory to derive fixed point equations which track the complete time evolution of the matrix-mean-square-error of the problem. The predictions of the resulting fixed point equations are validated by numerical experiments. In this short note we briefly illustrate a few predictions of our formalism by way of examples, and in particular we uncover continuous phase transitions in the extensive-rank and high-dimensional regime, which connect to the classical phase transitions of the low-rank problem in the appropriate limit. The formalism has much wider applicability than shown in this communication.

Gradient flow in the gaussian covariate model: exact solution of learning curves and multiple descent structures

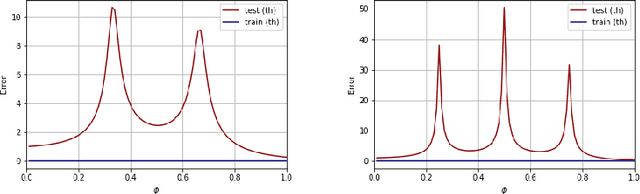
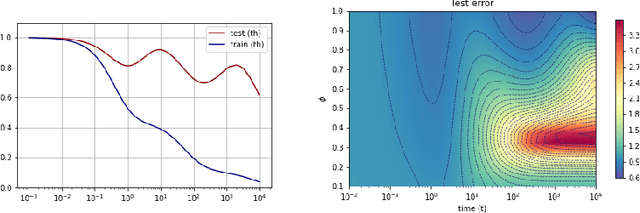
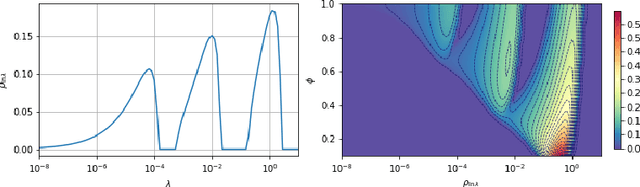
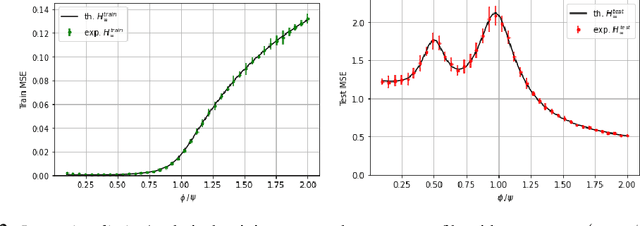
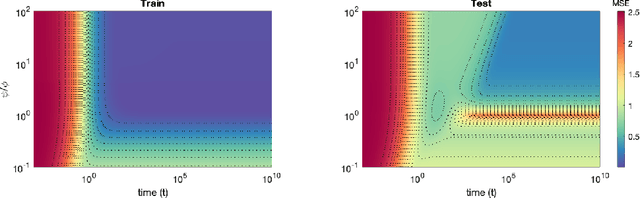
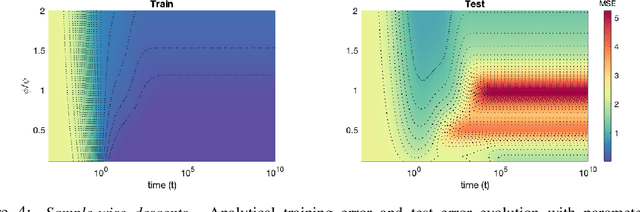
A recent line of work has shown remarkable behaviors of the generalization error curves in simple learning models. Even the least-squares regression has shown atypical features such as the model-wise double descent, and further works have observed triple or multiple descents. Another important characteristic are the epoch-wise descent structures which emerge during training. The observations of model-wise and epoch-wise descents have been analytically derived in limited theoretical settings (such as the random feature model) and are otherwise experimental. In this work, we provide a full and unified analysis of the whole time-evolution of the generalization curve, in the asymptotic large-dimensional regime and under gradient-flow, within a wider theoretical setting stemming from a gaussian covariate model. In particular, we cover most cases already disparately observed in the literature, and also provide examples of the existence of multiple descent structures as a function of a model parameter or time. Furthermore, we show that our theoretical predictions adequately match the learning curves obtained by gradient descent over realistic datasets. Technically we compute averages of rational expressions involving random matrices using recent developments in random matrix theory based on "linear pencils". Another contribution, which is also of independent interest in random matrix theory, is a new derivation of related fixed point equations (and an extension there-off) using Dyson brownian motions.

Model, sample, and epoch-wise descents: exact solution of gradient flow in the random feature model

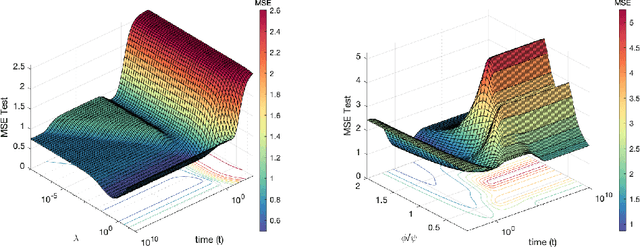
Recent evidence has shown the existence of a so-called double-descent and even triple-descent behavior for the generalization error of deep-learning models. This important phenomenon commonly appears in implemented neural network architectures, and also seems to emerge in epoch-wise curves during the training process. A recent line of research has highlighted that random matrix tools can be used to obtain precise analytical asymptotics of the generalization (and training) errors of the random feature model. In this contribution, we analyze the whole temporal behavior of the generalization and training errors under gradient flow for the random feature model. We show that in the asymptotic limit of large system size the full time-evolution path of both errors can be calculated analytically. This allows us to observe how the double and triple descents develop over time, if and when early stopping is an option, and also observe time-wise descent structures. Our techniques are based on Cauchy complex integral representations of the errors together with recent random matrix methods based on linear pencils.

Rank-one matrix estimation: analytic time evolution of gradient descent dynamics

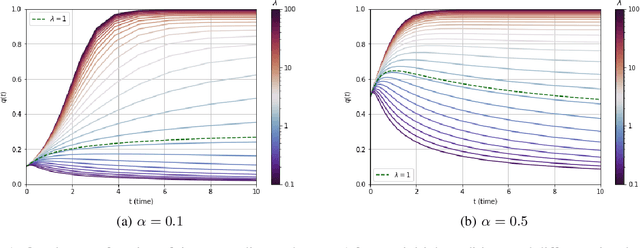
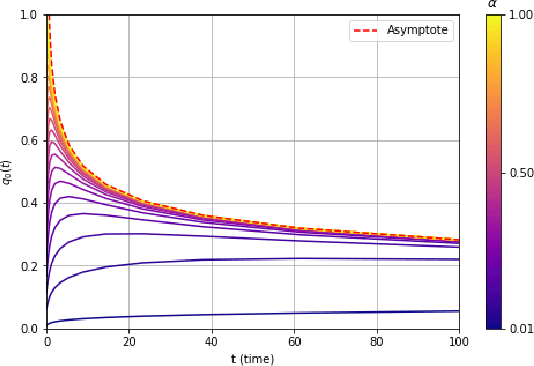
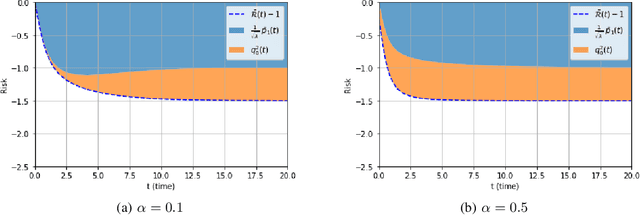
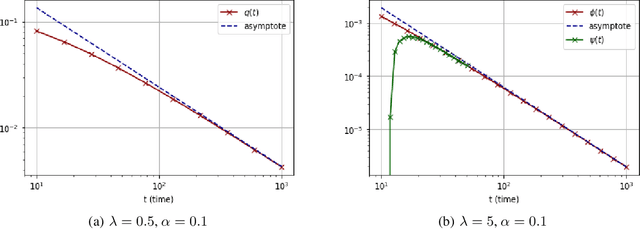
We consider a rank-one symmetric matrix corrupted by additive noise. The rank-one matrix is formed by an $n$-component unknown vector on the sphere of radius $\sqrt{n}$, and we consider the problem of estimating this vector from the corrupted matrix in the high dimensional limit of $n$ large, by gradient descent for a quadratic cost function on the sphere. Explicit formulas for the whole time evolution of the overlap between the estimator and unknown vector, as well as the cost, are rigorously derived. In the long time limit we recover the well known spectral phase transition, as a function of the signal-to-noise ratio. The explicit formulas also allow to point out interesting transient features of the time evolution. Our analysis technique is based on recent progress in random matrix theory and uses local versions of the semi-circle law.