Annika Lang
Short-term traffic prediction using physics-aware neural networks
Sep 21, 2021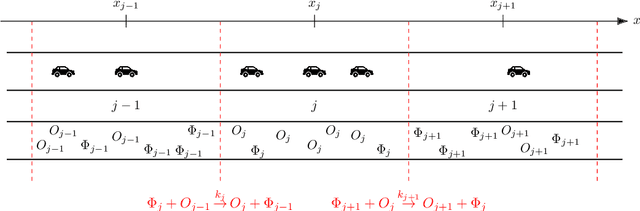
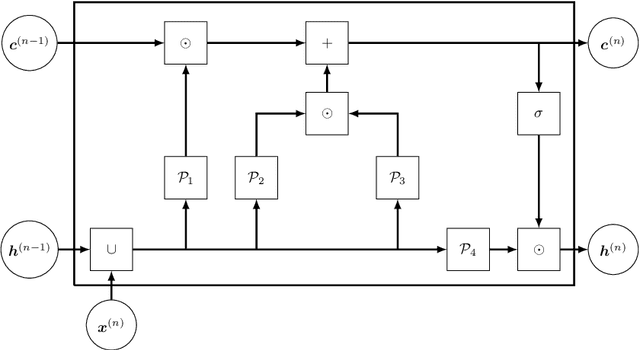

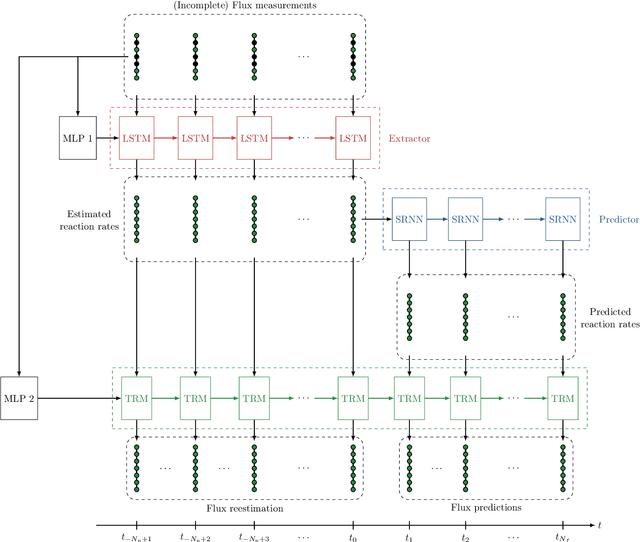
Abstract:In this work, we propose an algorithm performing short-term predictions of the flux of vehicles on a stretch of road, using past measurements of the flux. This algorithm is based on a physics-aware recurrent neural network. A discretization of a macroscopic traffic flow model (using the so-called Traffic Reaction Model) is embedded in the architecture of the network and yields flux predictions based on estimated and predicted space-time dependent traffic parameters. These parameters are themselves obtained using a succession of LSTM ans simple recurrent neural networks. Besides, on top of the predictions, the algorithm yields a smoothing of its inputs which is also physically-constrained by the macroscopic traffic flow model. The algorithm is tested on raw flux measurements obtained from loop detectors.
Parameter and density estimation from real-world traffic data: A kinetic compartmental approach
Jan 27, 2021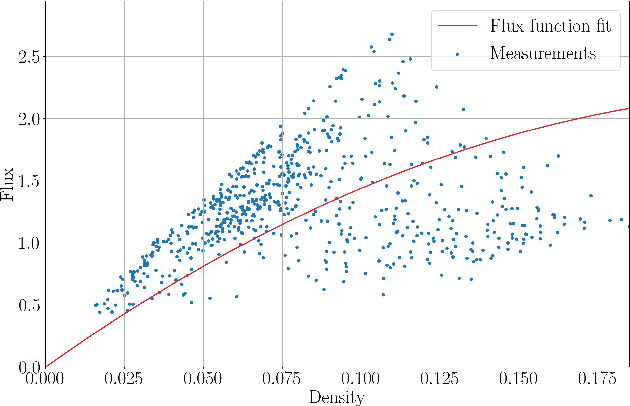
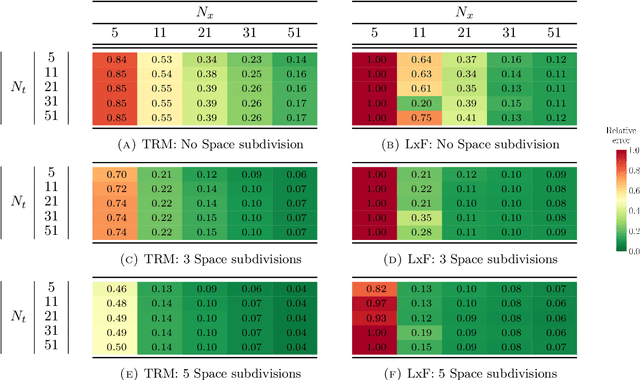
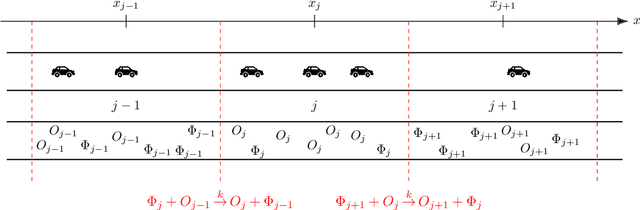
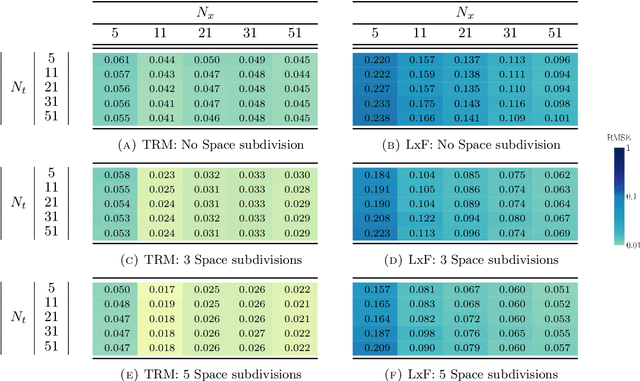
Abstract:The main motivation of this work is to assess the validity of a LWR traffic flow model to model measurements obtained from trajectory data, and propose extensions of this model to improve it. A formulation for a discrete dynamical system is proposed aiming at reproducing the evolution in time of the density of vehicles along a road, as observed in the measurements. This system is formulated as a chemical reaction network where road cells are interpreted as compartments, the transfer of vehicles from one cell to the other is seen as a chemical reaction between adjacent compartment and the density of vehicles is seen as a concentration of reactant. Several degrees of flexibility on the parameters of this system, which basically consist of the reaction rates between the compartments, can be considered: a constant value or a function depending on time and/or space. Density measurements coming from trajectory data are then interpreted as observations of the states of this system at consecutive times. Optimal reaction rates for the system are then obtained by minimizing the discrepancy between the output of the system and the state measurements. This approach was tested both on simulated and real data, proved successful in recreating the complexity of traffic flows despite the assumptions on the flux-density relation.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge