Obtaining A Linear Combination of the Principal Components of a Matrix on Quantum Computers

Principal component analysis is a multivariate statistical method frequently used in science and engineering to reduce the dimension of a problem or extract the most significant features from a dataset. In this paper, using a similar notion to the quantum counting, we show how to apply the amplitude amplification together with the phase estimation algorithm to an operator in order to procure the eigenvectors of the operator associated to the eigenvalues defined in the range $\left[a, b\right]$, where $a$ and $b$ are real and $0 \leq a \leq b \leq 1$. This makes possible to obtain a combination of the eigenvectors associated to the largest eigenvalues and so can be used to do principal component analysis on quantum computers.

Group Leaders Optimization Algorithm

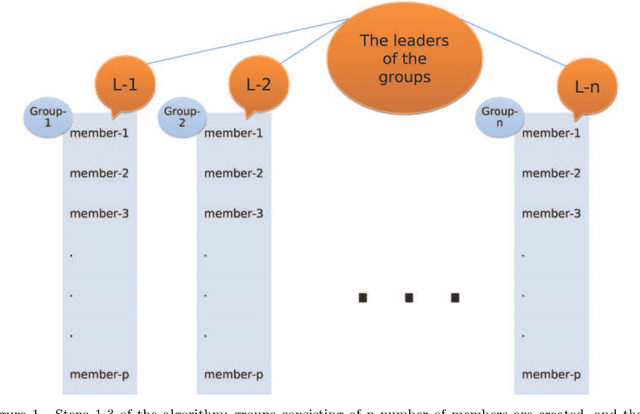
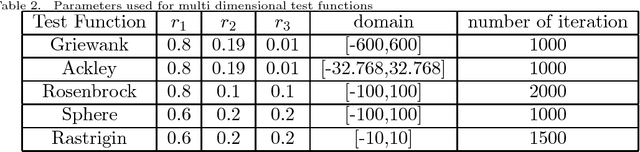
We present a new global optimization algorithm in which the influence of the leaders in social groups is used as an inspiration for the evolutionary technique which is designed into a group architecture. To demonstrate the efficiency of the method, a standard suite of single and multidimensional optimization functions along with the energies and the geometric structures of Lennard-Jones clusters are given as well as the application of the algorithm on quantum circuit design problems. We show that as an improvement over previous methods, the algorithm scales as N^2.5 for the Lennard-Jones clusters of N-particles. In addition, an efficient circuit design is shown for two qubit Grover search algorithm which is a quantum algorithm providing quadratic speed-up over the classical counterpart.