Andrew J. Majda
Nonlinear Laplacian spectral analysis: Capturing intermittent and low-frequency spatiotemporal patterns in high-dimensional data
Jul 17, 2012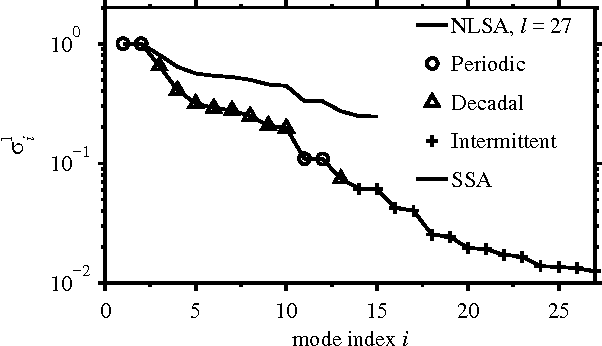
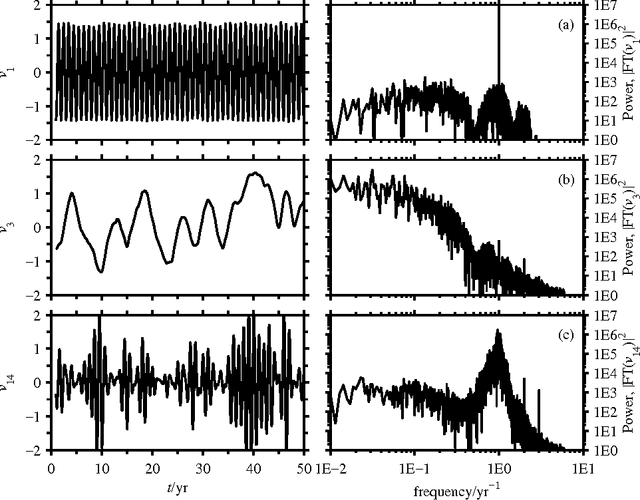
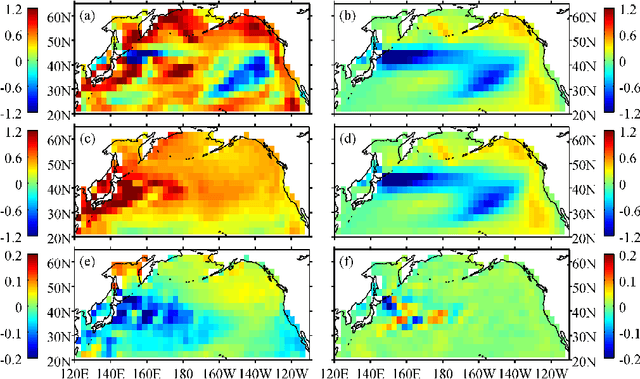
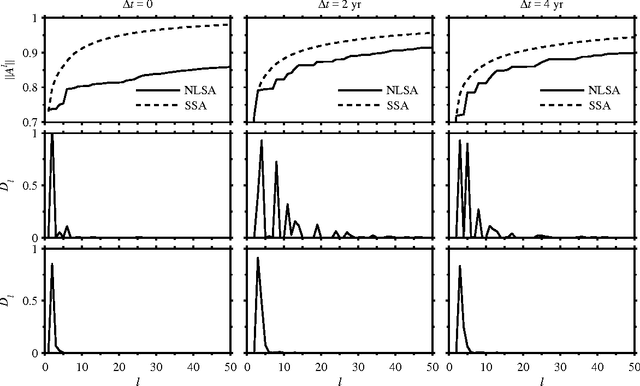
Abstract:We present a technique for spatiotemporal data analysis called nonlinear Laplacian spectral analysis (NLSA), which generalizes singular spectrum analysis (SSA) to take into account the nonlinear manifold structure of complex data sets. The key principle underlying NLSA is that the functions used to represent temporal patterns should exhibit a degree of smoothness on the nonlinear data manifold M; a constraint absent from classical SSA. NLSA enforces such a notion of smoothness by requiring that temporal patterns belong in low-dimensional Hilbert spaces V_l spanned by the leading l Laplace-Beltrami eigenfunctions on M. These eigenfunctions can be evaluated efficiently in high ambient-space dimensions using sparse graph-theoretic algorithms. Moreover, they provide orthonormal bases to expand a family of linear maps, whose singular value decomposition leads to sets of spatiotemporal patterns at progressively finer resolution on the data manifold. The Riemannian measure of M and an adaptive graph kernel width enhances the capability of NLSA to detect important nonlinear processes, including intermittency and rare events. The minimum dimension of V_l required to capture these features while avoiding overfitting is estimated here using spectral entropy criteria.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge