Soft regression trees: a model variant and a decomposition training algorithm

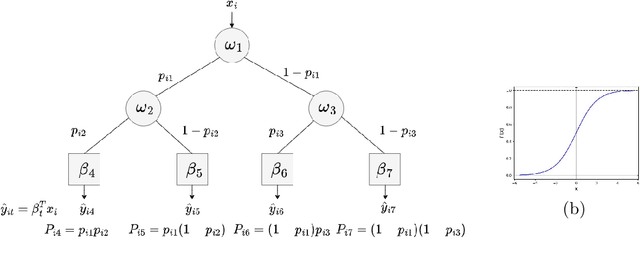
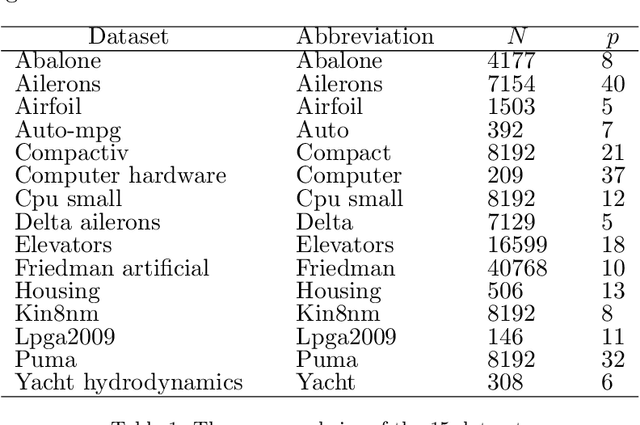
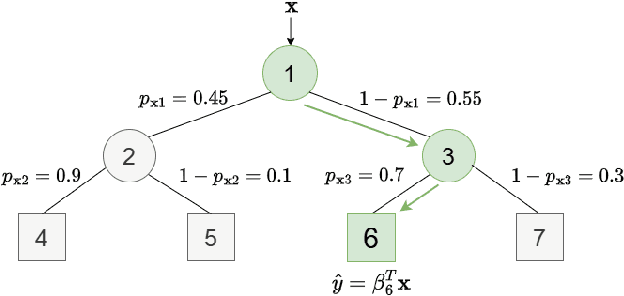
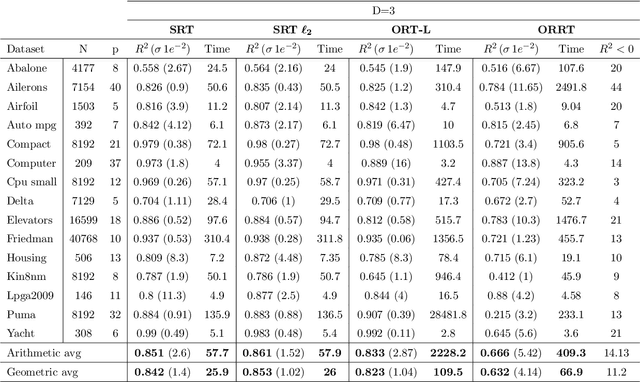
Decision trees are widely used for classification and regression tasks in a variety of application fields due to their interpretability and good accuracy. During the past decade, growing attention has been devoted to globally optimized decision trees with deterministic or soft splitting rules at branch nodes, which are trained by optimizing the error function over all the tree parameters. In this work, we propose a new variant of soft multivariate regression trees (SRTs) where, for every input vector, the prediction is defined as the linear regression associated to a single leaf node, namely, the leaf node obtained by routing the input vector from the root along the branches with higher probability. SRTs exhibit the conditional computational property, i.e., each prediction depends on a small number of nodes (parameters), and our nonlinear optimization formulation for training them is amenable to decomposition. After showing a universal approximation result for SRTs, we present a decomposition training algorithm including a clustering-based initialization procedure and a heuristic for reassigning the input vectors along the tree. Under mild assumptions, we establish asymptotic convergence guarantees. Experiments on 15 wellknown datasets indicate that our SRTs and decomposition algorithm yield higher accuracy and robustness compared with traditional soft regression trees trained using the nonlinear optimization formulation of Blanquero et al., and a significant reduction in training times as well as a slightly better average accuracy compared with the mixed-integer optimization approach of Bertsimas and Dunn. We also report a comparison with the Random Forest ensemble method.

On multivariate randomized classification trees: $l_0$-based sparsity, VC~dimension and decomposition methods

Decision trees are widely-used classification and regression models because of their interpretability and good accuracy. Classical methods such as CART are based on greedy approaches but a growing attention has recently been devoted to optimal decision trees. We investigate the nonlinear continuous optimization formulation proposed in Blanquero et al. (EJOR, vol. 284, 2020; COR, vol. 132, 2021) for (sparse) optimal randomized classification trees. Sparsity is important not only for feature selection but also to improve interpretability. We first consider alternative methods to sparsify such trees based on concave approximations of the $l_{0}$ ``norm". Promising results are obtained on 24 datasets in comparison with $l_1$ and $l_{\infty}$ regularizations. Then, we derive bounds on the VC dimension of multivariate randomized classification trees. Finally, since training is computationally challenging for large datasets, we propose a general decomposition scheme and an efficient version of it. Experiments on larger datasets show that the proposed decomposition method is able to significantly reduce the training times without compromising the accuracy.