Ancestral Inference and Learning for Branching Processes in Random Environments

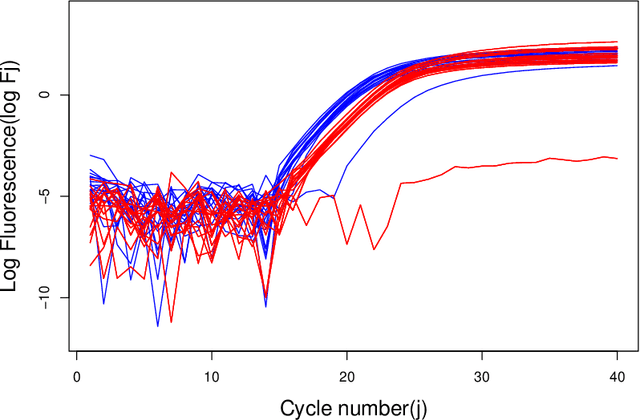
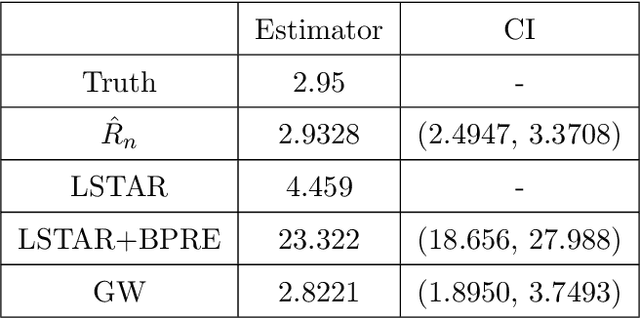
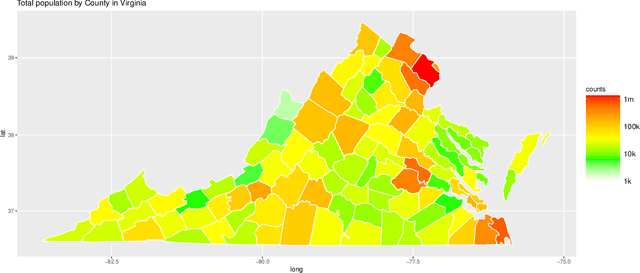
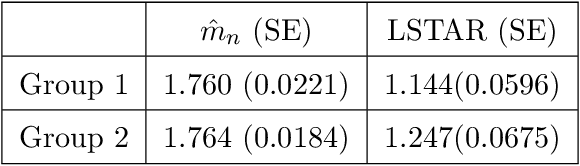
Ancestral inference for branching processes in random environments involves determining the ancestor distribution parameters using the population sizes of descendant generations. In this paper, we introduce a new methodology for ancestral inference utilizing the generalized method of moments. We demonstrate that the estimator's behavior is critically influenced by the coefficient of variation of the environment sequence. Furthermore, despite the process's evolution being heavily dependent on the offspring means of various generations, we show that the joint limiting distribution of the ancestor and offspring estimators of the mean, under appropriate centering and scaling, decouple and converge to independent Gaussian random variables when the ratio of the number of generations to the logarithm of the number of replicates converges to zero. Additionally, we provide estimators for the limiting variance and illustrate our findings through numerical experiments and data from Polymerase Chain Reaction experiments and COVID-19 data.

Private Minimum Hellinger Distance Estimation via Hellinger Distance Differential Privacy

Hellinger distance has been widely used to derive objective functions that are alternatives to maximum likelihood methods. Motivated by recent regulatory privacy requirements, estimators satisfying differential privacy constraints are being derived. In this paper, we describe different notions of privacy using divergences and establish that Hellinger distance minimizes the added variance within the class of power divergences for an additive Gaussian mechanism. We demonstrate that a new definition of privacy, namely Hellinger differential privacy, shares several features of the standard notion of differential privacy while allowing for sharper inference. Using these properties, we develop private versions of gradient descent and Newton-Raphson algorithms for obtaining private minimum Hellinger distance estimators, which are robust and first-order efficient. Using numerical experiments, we illustrate the finite sample performance and verify that they retain their robustness properties under gross-error contamination.