Consistent causal discovery with equal error variances: a least-squares perspective

We consider the problem of recovering the true causal structure among a set of variables, generated by a linear acyclic structural equation model (SEM) with the error terms being independent and having equal variances. It is well-known that the true underlying directed acyclic graph (DAG) encoding the causal structure is uniquely identifiable under this assumption. In this work, we establish that the sum of minimum expected squared errors for every variable, while predicted by the best linear combination of its parent variables, is minimised if and only if the causal structure is represented by any supergraph of the true DAG. This property is further utilised to design a Bayesian DAG selection method that recovers the true graph consistently.

A Cross Validation Framework for Signal Denoising with Applications to Trend Filtering, Dyadic CART and Beyond

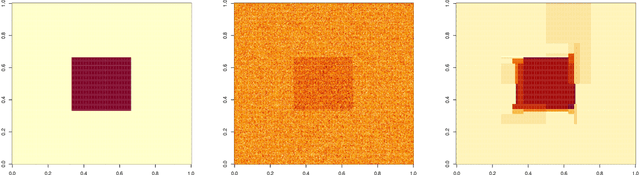
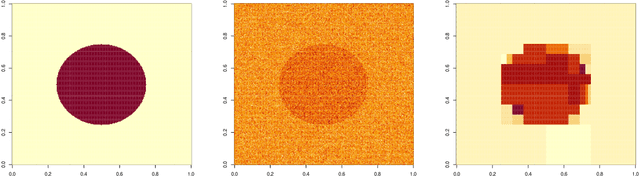
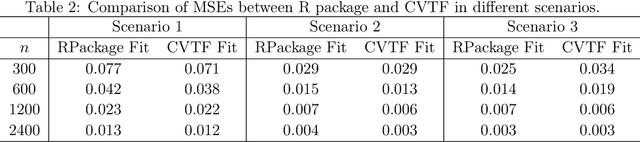
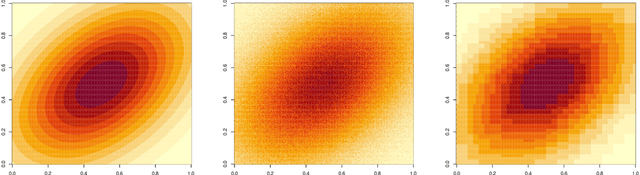
This paper formulates a general cross validation framework for signal denoising. The general framework is then applied to nonparametric regression methods such as Trend Filtering and Dyadic CART. The resulting cross validated versions are then shown to attain nearly the same rates of convergence as are known for the optimally tuned analogues. There did not exist any previous theoretical analyses of cross validated versions of Trend Filtering or Dyadic CART. To illustrate the generality of the framework we also propose and study cross validated versions of two fundamental estimators; lasso for high dimensional linear regression and singular value thresholding for matrix estimation. Our general framework is inspired by the ideas in Chatterjee and Jafarov (2015) and is potentially applicable to a wide range of estimation methods which use tuning parameters.