Get our free extension to see links to code for papers anywhere online!Free add-on: code for papers everywhere!Free add-on: See code for papers anywhere!
Alex Kaltenbach
The Deep Ritz Method for Parametric $p$-Dirichlet Problems
Jul 05, 2022Figures and Tables: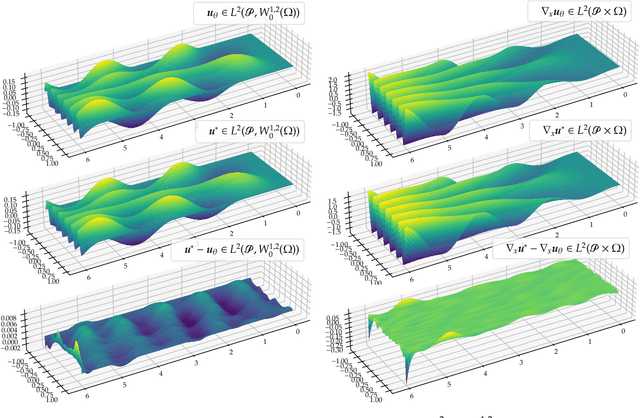
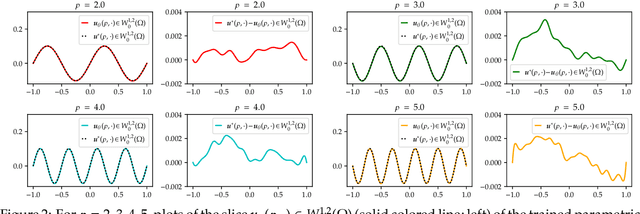
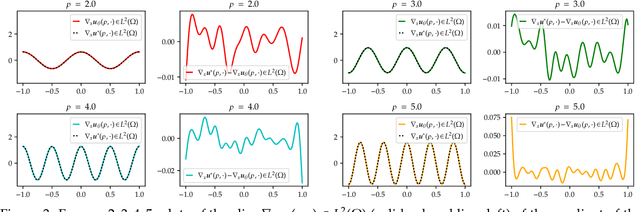
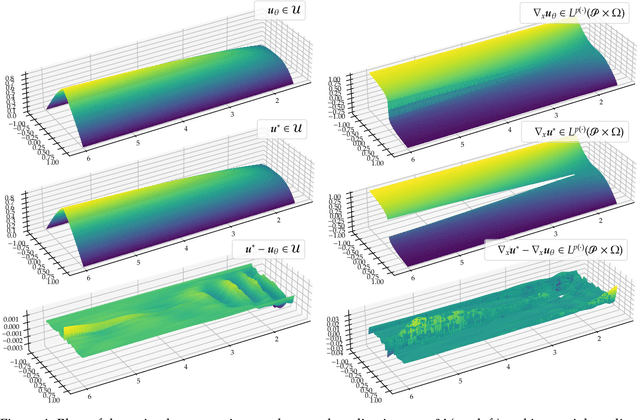




Abstract:We establish error estimates for the approximation of parametric $p$-Dirichlet problems deploying the Deep Ritz Method. Parametric dependencies include, e.g., varying geometries and exponents $p\in (1,\infty)$. Combining the derived error estimates with quantitative approximation theorems yields error decay rates and establishes that the Deep Ritz Method retains the favorable approximation capabilities of neural networks in the approximation of high dimensional functions which makes the method attractive for parametric problems. Finally, we present numerical examples to illustrate potential applications.
* 30 pages, 11 figures
Via
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge