Alejandro Morán
Reservoir Computing Hardware with Cellular Automata
Jun 21, 2018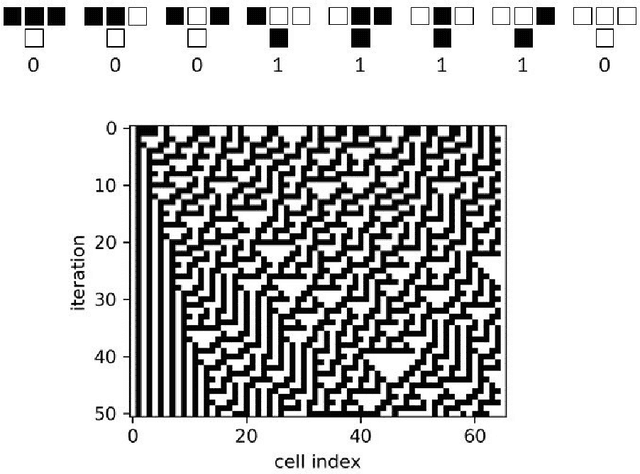
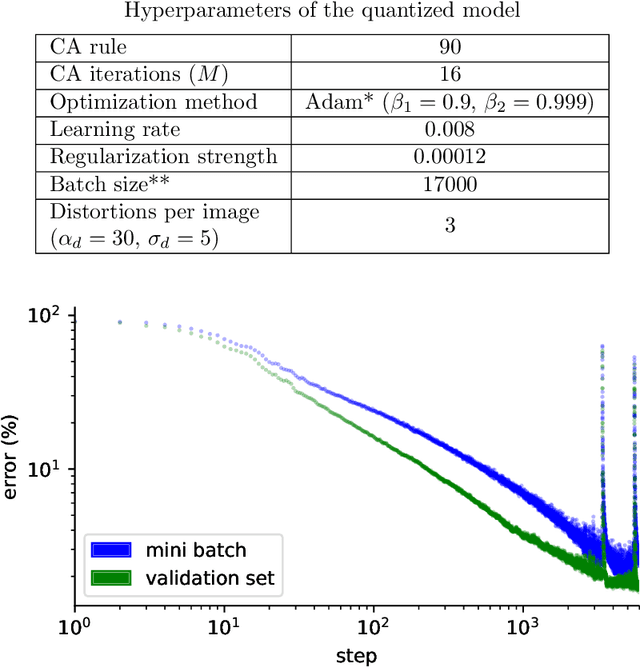
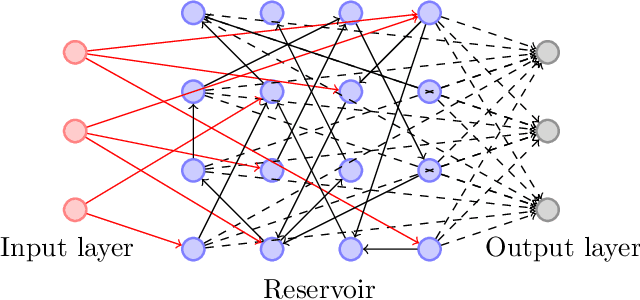
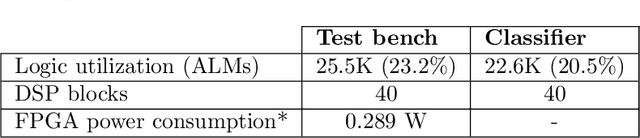
Abstract:Elementary cellular automata (ECA) is a widely studied one-dimensional processing methodology where the successive iteration of the automaton may lead to the recreation of a rich pattern dynamic. Recently, cellular automata have been proposed as a feasible way to implement Reservoir Computing (RC) systems in which the automata rule is fixed and the training is performed using a linear regression. In this work we perform an exhaustive study of the performance of the different ECA rules when applied to pattern recognition of time-independent input signals using a RC scheme. Once the different ECA rules have been tested, the most accurate one (rule 90) is selected to implement a digital circuit. Rule 90 is easily reproduced using a reduced set of XOR gates and shift-registers, thus representing a high-performance alternative for RC hardware implementation in terms of processing time, circuit area, power dissipation and system accuracy. The model (both in software and its hardware implementation) has been tested using a pattern recognition task of handwritten numbers (the MNIST database) for which we obtained competitive results in terms of accuracy, speed and power dissipation. The proposed model can be considered to be a low-cost method to implement fast pattern recognition digital circuits.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge