Simulating the Effects of Eco-Friendly Transportation Selections for Air Pollution Reduction

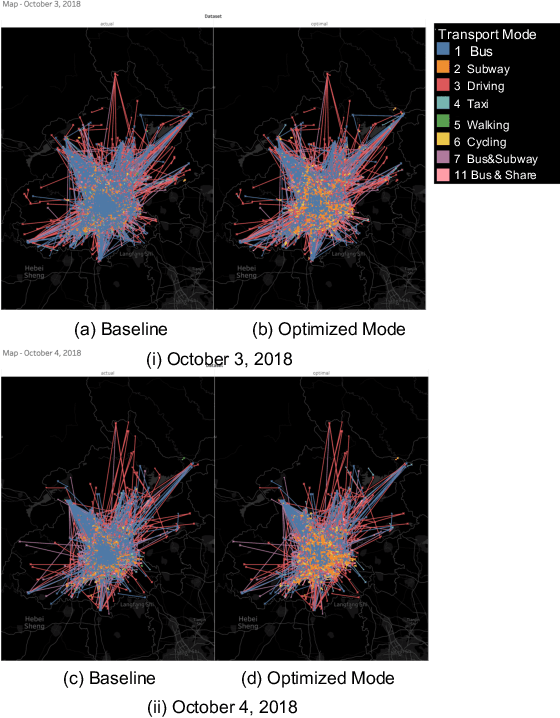
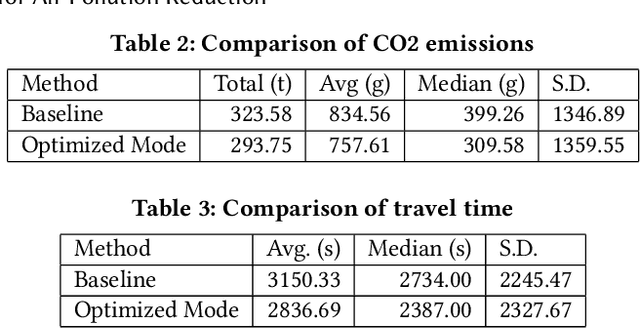
Reducing air pollution, such as CO2 and PM2.5 emissions, is one of the most important issues for many countries worldwide. Selecting an environmentally friendly transport mode can be an effective approach of individuals to reduce air pollution in daily life. In this study, we propose a method to simulate the effectiveness of an eco-friendly transport mode selection for reducing air pollution by using map search logs. We formulate the transport mode selection as a combinatorial optimization problem with the constraints regarding the total amount of CO2 emissions as an example of air pollution and the average travel time. The optimization results show that the total amount of CO2 emissions can be reduced by 9.23%, whereas the average travel time can in fact be reduced by 9.96%. Our research proposal won first prize in Regular Machine Learning Competition Track Task 2 at KDD Cup 2019.

Trading Transforms of Non-weighted Simple Games and Integer Weights of Weighted Simple Games

This paper is concerned with simple games. One of the fundamental questions regarding simple games is that of what makes a simple game a weighted majority game. Taylor and Zwicker (1992) showed that a simple game is non-weighted if and only if there exists a trading transform of finite size. They also provided an upper bound on the size of such a trading transform, if it exists. Gvozdeva and Slinko (2009) improved on that upper bound. Their proof employs a property of linear inequalities demonstrated by Muroga (1971). We provide a new proof of the existence of a trading transform when a given simple game is non-weighted. Our proof employs Farkas' lemma (1894), and yields an improved upper bound on the size of a trading transform. We also discuss an integer weights representation of a weighted simple game, and improve on the bounds obtained by Muroga (1971). We show that our bounds are tight when the number of players is less than or equal to five, based on the computational results obtained by Kurz (2012). Lastly, we deal with the problem of finding an integer weights representation under the assumption that we have minimal winning coalitions and maximal losing coalitions. We discuss a performance of a rounding method.