Using Machine Learning and Neural Networks to Analyze and Predict Chaos in Multi-Pendulum and Chaotic Systems

A chaotic system is a highly volatile system characterized by its sensitive dependence on initial conditions and outside factors. Chaotic systems are prevalent throughout the world today: in weather patterns, disease outbreaks, and even financial markets. Chaotic systems are seen in every field of science and humanities, so being able to predict these systems is greatly beneficial to society. In this study, we evaluate 10 different machine learning models and neural networks [1] based on Root Mean Squared Error (RMSE) and R^2 values for their ability to predict one of these systems, the multi-pendulum. We begin by generating synthetic data representing the angles of the pendulum over time using the Runge Kutta Method for solving 4th Order Differential Equations (ODE-RK4) [2]. At first, we used the single-step sliding window approach, predicting the 50st step after training for steps 0-49 and so forth. However, to more accurately cover chaotic motion and behavior in these systems, we transitioned to a time-step based approach. Here, we trained the model/network on many initial angles and tested it on a completely new set of initial angles, or 'in-between' to capture chaotic motion to its fullest extent. We also evaluated the stability of the system using Lyapunov exponents. We concluded that for a double pendulum, the best model was the Long Short Term Memory Network (LSTM)[3] for the sliding window and time step approaches in both friction and frictionless scenarios. For triple pendulum, the Vanilla Recurrent Neural Network (VRNN)[4] was the best for the sliding window and Gated Recurrent Network (GRU) [5] was the best for the time step approach, but for friction, LSTM was the best.

A physics-informed search for metric solutions to Ricci flow, their embeddings, and visualisation

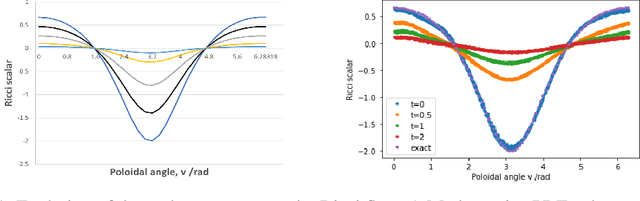
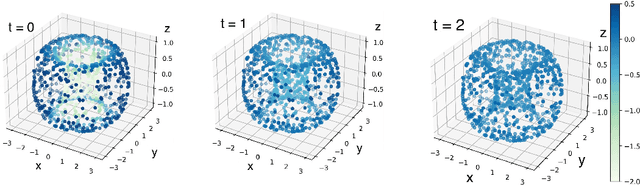
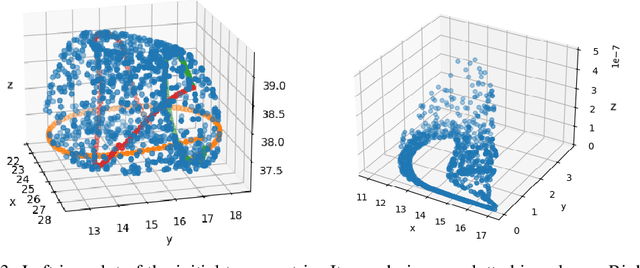
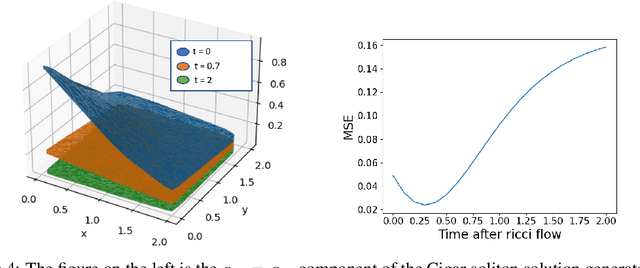
Neural networks with PDEs embedded in their loss functions (physics-informed neural networks) are employed as a function approximators to find solutions to the Ricci flow (a curvature based evolution) of Riemannian metrics. A general method is developed and applied to the real torus. The validity of the solution is verified by comparing the time evolution of scalar curvature with that found using a standard PDE solver, which decreases to a constant value of 0 on the whole manifold. We also consider certain solitonic solutions to the Ricci flow equation in two real dimensions. We create visualisations of the flow by utilising an embedding into $\mathbb{R}^3$. Snapshots of highly accurate numerical evolution of the toroidal metric over time are reported. We provide guidelines on applications of this methodology to the problem of determining Ricci flat Calabi--Yau metrics in the context of String theory, a long standing problem in complex geometry.