Winograd Convolution for DNNs: Beyond linear polinomials

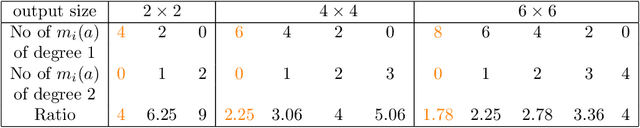
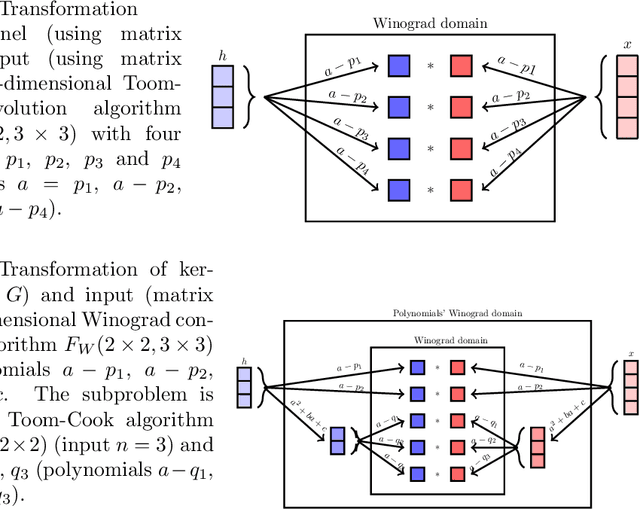
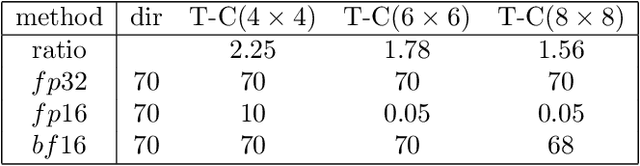
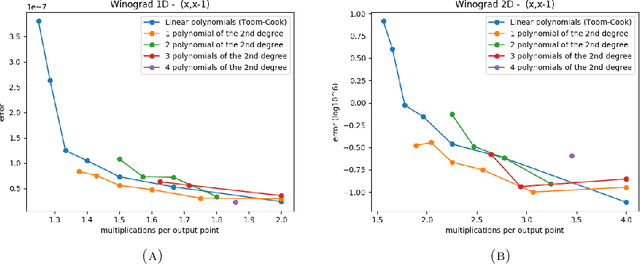
We investigated a wider range of Winograd family convolution algorithms for Deep Neural Network. We presented the explicit Winograd convolution algorithm in general case (used the polynomials of the degrees higher than one). It allows us to construct more different versions in the aspect of performance than commonly used Winograd convolution algorithms and improve the accuracy and performance of convolution computations. We found that in $fp16$ this approach gives us better accuracy of image recognition while keeps the same number of general multiplications computed per single output point as the commonly used Winograd algorithm for a kernel of the size $3 \times 3$ and output size equal to $4 \times 4$. We demonstrated that in $bf16$ it is possible to perform the convolution computation faster keeping the accuracy of image recognition the same as for direct convolution method. We tested our approach for a subset of $2000$ images from Imaginet validation set. We present the results for three precision of computations $fp32$, $fp16$ and $bf16$.