Will My Robot Achieve My Goals? Predicting the Probability that an MDP Policy Reaches a User-Specified Behavior Target

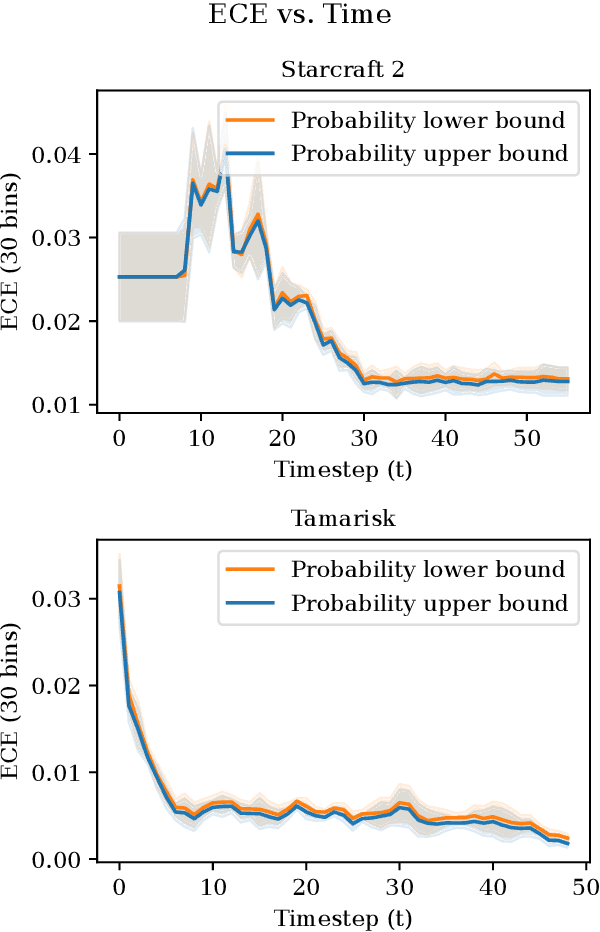
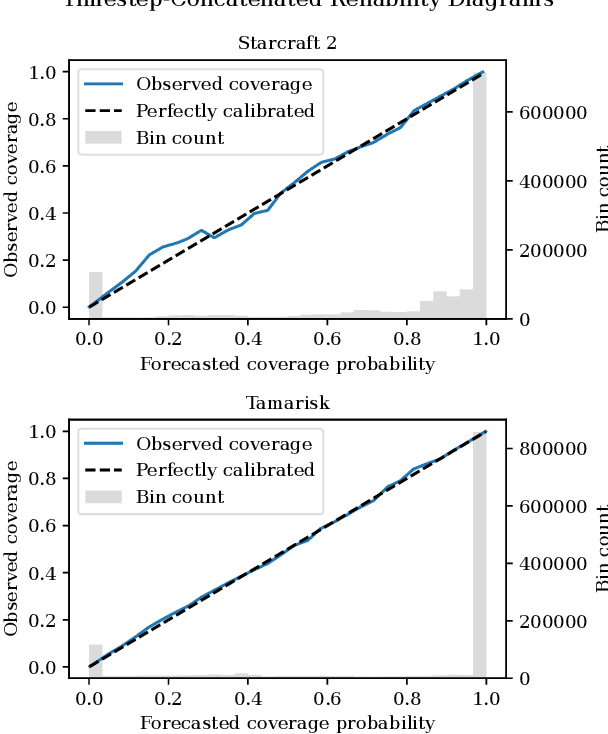
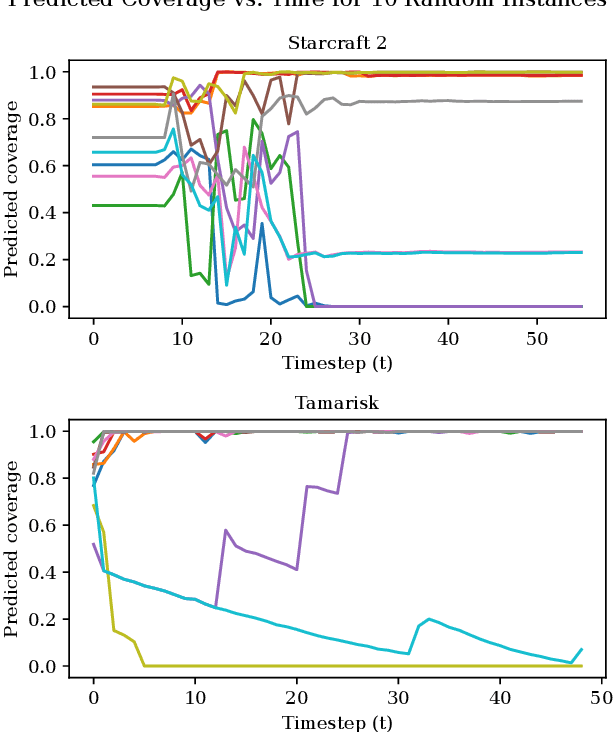
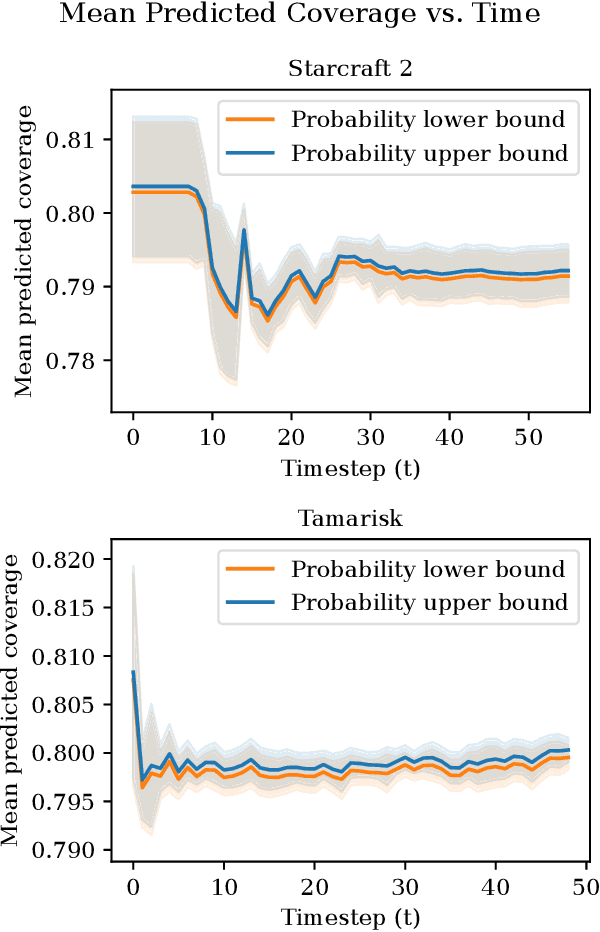
As an autonomous system performs a task, it should maintain a calibrated estimate of the probability that it will achieve the user's goal. If that probability falls below some desired level, it should alert the user so that appropriate interventions can be made. This paper considers settings where the user's goal is specified as a target interval for a real-valued performance summary, such as the cumulative reward, measured at a fixed horizon $H$. At each time $t \in \{0, \ldots, H-1\}$, our method produces a calibrated estimate of the probability that the final cumulative reward will fall within a user-specified target interval $[y^-,y^+].$ Using this estimate, the autonomous system can raise an alarm if the probability drops below a specified threshold. We compute the probability estimates by inverting conformal prediction. Our starting point is the Conformalized Quantile Regression (CQR) method of Romano et al., which applies split-conformal prediction to the results of quantile regression. CQR is not invertible, but by using the conditional cumulative distribution function (CDF) as the non-conformity measure, we show how to obtain an invertible modification that we call \textbf{P}robability-space \textbf{C}onformalized \textbf{Q}uantile \textbf{R}egression (PCQR). Like CQR, PCQR produces well-calibrated conditional prediction intervals with finite-sample marginal guarantees. By inverting PCQR, we obtain marginal guarantees for the probability that the cumulative reward of an autonomous system will fall within an arbitrary user-specified target intervals. Experiments on two domains confirm that these probabilities are well-calibrated.