When and how epochwise double descent happens
Paper and Code
Aug 26, 2021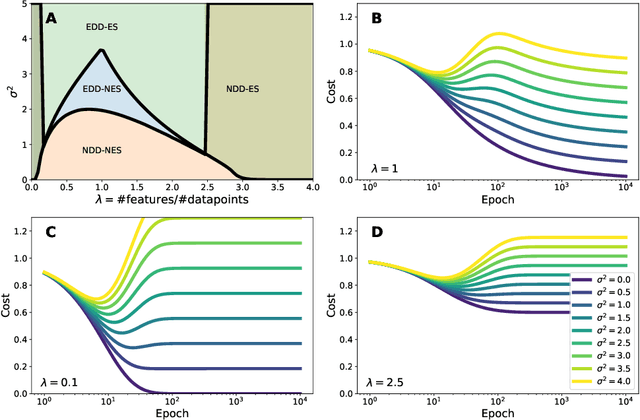
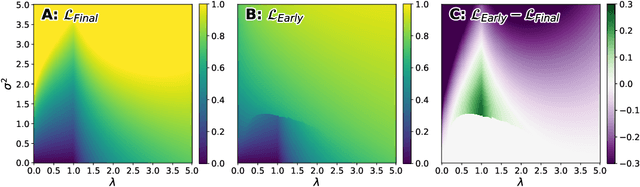
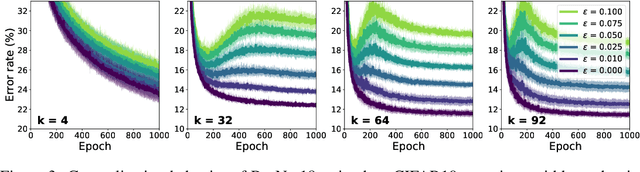
Deep neural networks are known to exhibit a `double descent' behavior as the number of parameters increases. Recently, it has also been shown that an `epochwise double descent' effect exists in which the generalization error initially drops, then rises, and finally drops again with increasing training time. This presents a practical problem in that the amount of time required for training is long, and early stopping based on validation performance may result in suboptimal generalization. In this work we develop an analytically tractable model of epochwise double descent that allows us to characterise theoretically when this effect is likely to occur. This model is based on the hypothesis that the training data contains features that are slow to learn but informative. We then show experimentally that deep neural networks behave similarly to our theoretical model. Our findings indicate that epochwise double descent requires a critical amount of noise to occur, but above a second critical noise level early stopping remains effective. Using insights from theory, we give two methods by which epochwise double descent can be removed: one that removes slow to learn features from the input and reduces generalization performance, and another that instead modifies the training dynamics and matches or exceeds the generalization performance of standard training. Taken together, our results suggest a new picture of how epochwise double descent emerges from the interplay between the dynamics of training and noise in the training data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge