Warped Convolution Networks for Homography Estimation
Paper and Code
Jun 23, 2022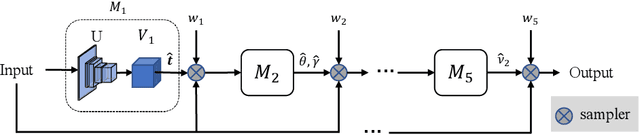
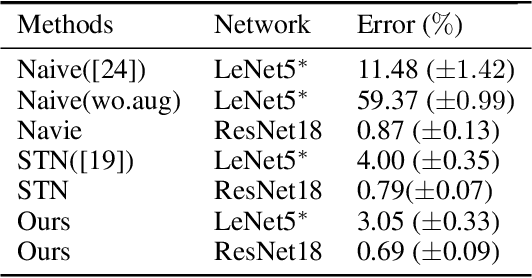


Homography transformation has an essential relationship with special linear group and the embedding Lie algebra structure. Although the Lie algebra representation is elegant, few researchers have established the connection between homography estimation and algebra expression. In this paper, we propose Warped Convolution Networks (WCN) to effectively estimate the homography transformation by SL(3) group and sl(3) algebra with group convolution. To this end, six commutative subgroups within SL(3) group are composed to form a homography transformation. For each subgroup, a warping function is proposed to bridge the Lie algebra structure to its corresponding parameters in tomography. By taking advantage of the warped convolution, homography estimation is formulated into several simple pseudo-translation regressions. By walking along the Lie topology, our proposed WCN is able to learn the features that are invariant to homography transformation. It can be easily plugged into other popular CNN-based methods. Extensive experiments on POT benchmark and MNIST-Proj dataset show that our proposed method is effective for both homography estimation and classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge