Very Efficient Training of Convolutional Neural Networks using Fast Fourier Transform and Overlap-and-Add
Paper and Code
Jan 25, 2016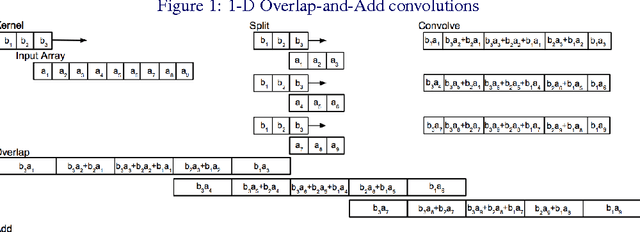


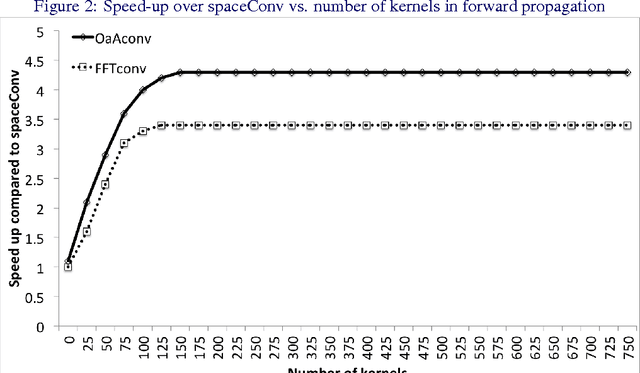
Convolutional neural networks (CNNs) are currently state-of-the-art for various classification tasks, but are computationally expensive. Propagating through the convolutional layers is very slow, as each kernel in each layer must sequentially calculate many dot products for a single forward and backward propagation which equates to $\mathcal{O}(N^{2}n^{2})$ per kernel per layer where the inputs are $N \times N$ arrays and the kernels are $n \times n$ arrays. Convolution can be efficiently performed as a Hadamard product in the frequency domain. The bottleneck is the transformation which has a cost of $\mathcal{O}(N^{2}\log_2 N)$ using the fast Fourier transform (FFT). However, the increase in efficiency is less significant when $N\gg n$ as is the case in CNNs. We mitigate this by using the "overlap-and-add" technique reducing the computational complexity to $\mathcal{O}(N^2\log_2 n)$ per kernel. This method increases the algorithm's efficiency in both the forward and backward propagation, reducing the training and testing time for CNNs. Our empirical results show our method reduces computational time by a factor of up to 16.3 times the traditional convolution implementation for a 8 $\times$ 8 kernel and a 224 $\times$ 224 image.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge