Variational Bayes: A report on approaches and applications
Paper and Code
May 26, 2019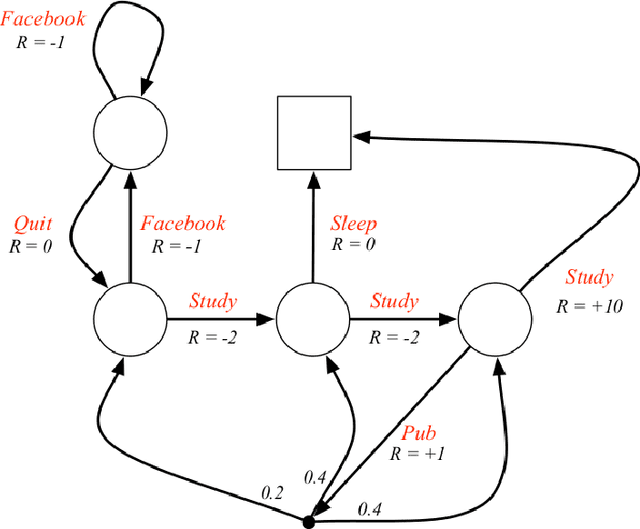
Deep neural networks have achieved impressive results on a wide variety of tasks. However, quantifying uncertainty in the network's output is a challenging task. Bayesian models offer a mathematical framework to reason about model uncertainty. Variational methods have been used for approximating intractable integrals that arise in Bayesian inference for neural networks. In this report, we review the major variational inference concepts pertinent to Bayesian neural networks and compare various approximation methods used in literature. We also talk about the applications of variational bayes in Reinforcement learning and continual learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge