Using Quantum Computing to Infer Dynamic Behaviors of Biological and Artificial Neural Networks

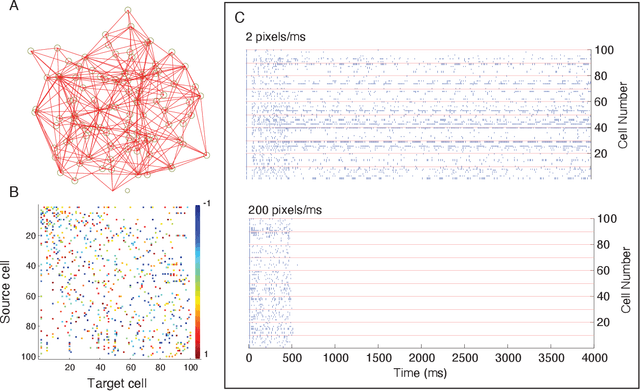
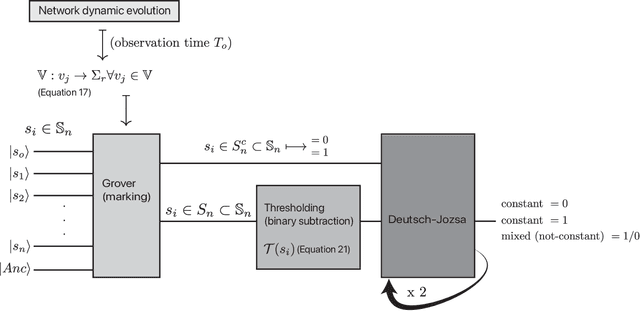
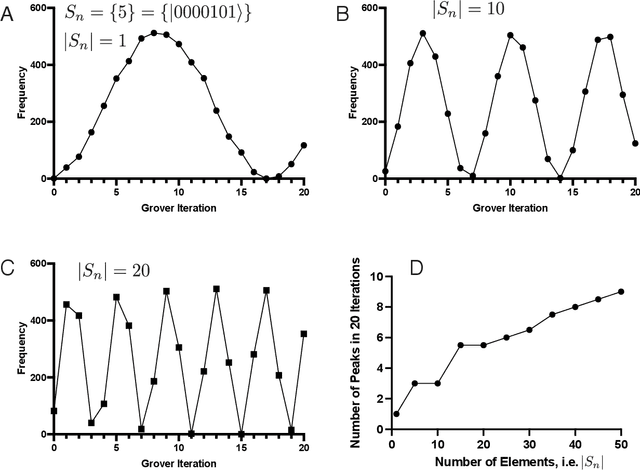
The exploration of new problem classes for quantum computation is an active area of research. An essentially completely unexplored topic is the use of quantum algorithms and computing to explore and ask questions \textit{about} the functional dynamics of neural networks. This is a component of the still-nascent topic of applying quantum computing to the modeling and simulations of biological and artificial neural networks. In this work, we show how a carefully constructed set of conditions can use two foundational quantum algorithms, Grover and Deutsch-Josza, in such a way that the output measurements admit an interpretation that guarantees we can infer if a simple representation of a neural network (which applies to both biological and artificial networks) after some period of time has the potential to continue sustaining dynamic activity. Or whether the dynamics are guaranteed to stop either through 'epileptic' dynamics or quiescence.