Unsupervised Embedding of Hierarchical Structure in Euclidean Space
Paper and Code
Oct 30, 2020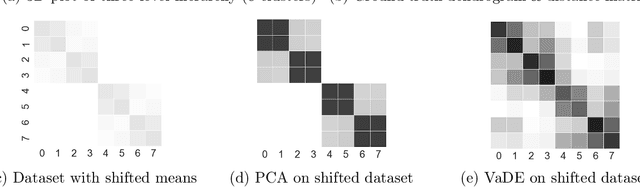


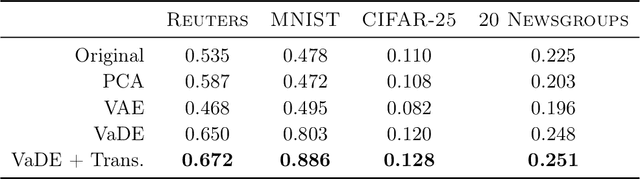
Deep embedding methods have influenced many areas of unsupervised learning. However, the best methods for learning hierarchical structure use non-Euclidean representations, whereas Euclidean geometry underlies the theory behind many hierarchical clustering algorithms. To bridge the gap between these two areas, we consider learning a non-linear embedding of data into Euclidean space as a way to improve the hierarchical clustering produced by agglomerative algorithms. To learn the embedding, we revisit using a variational autoencoder with a Gaussian mixture prior, and we show that rescaling the latent space embedding and then applying Ward's linkage-based algorithm leads to improved results for both dendrogram purity and the Moseley-Wang cost function. Finally, we complement our empirical results with a theoretical explanation of the success of this approach. We study a synthetic model of the embedded vectors and prove that Ward's method exactly recovers the planted hierarchical clustering with high probability.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge