Unrolled Wirtinger Flow with Deep Priors for Phaseless Imaging

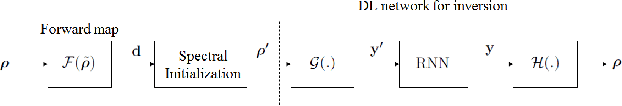
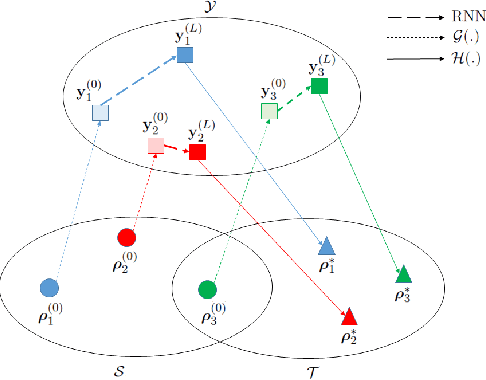
We introduce a deep learning (DL) based network for imaging from measurement intensities. The network architecture uses a recurrent structure that unrolls the Wirtinger Flow (WF) algorithm with a deep prior which enables performing the algorithm updates in a lower dimensional encoded image space. We use a separate deep network (DN), referred to as the encoding network, for transforming the spectral initialization used in the WF algorithm to an appropriate initial value for the encoded domain. The unrolling scheme that models a fixed number of iterations of the underlying algorithm into a recurrent neural network (RNN) enable us to simultaneously learn the parameters of the prior network, the encoding network and the RNN during training. We establish sufficient conditions on the network to guarantee exact recovery under deterministic forward models and demonstrate the relation between the Lipschitz constants of the trained prior and encoding networks to the convergence rate. We show the practical applicability of our method on synthetic aperture imaging using high fidelity simulation data from the PCSWAT software. Our numerical study shows that the deep prior facilitates improvements in sample complexity.