Training Neural Networks Using the Property of Negative Feedback to Inverse a Function
Paper and Code
Mar 25, 2021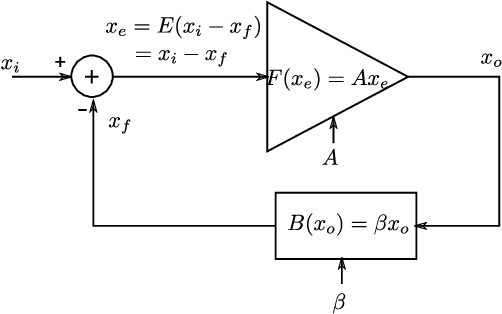
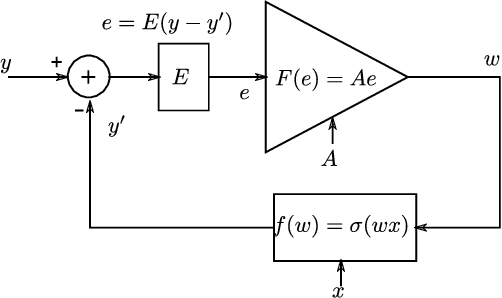

With high forward gain, a negative feedback system has the ability to perform the inverse of a linear or non linear function that is in the feedback path. This property of negative feedback systems has been widely used in analog circuits to construct precise closed-loop functions. This paper describes how the property of a negative feedback system to perform inverse of a function can be used for training neural networks. This method does not require that the cost or activation functions be differentiable. Hence, it is able to learn a class of non-differentiable functions as well where a gradient descent-based method fails. We also show that gradient descent emerges as a special case of the proposed method. We have applied this method to the MNIST dataset and obtained results that shows the method is viable for neural network training. This method, to the best of our knowledge, is novel in machine learning.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge