Training L1-Regularized Models with Orthant-Wise Passive Descent Algorithms
Paper and Code
Feb 22, 2018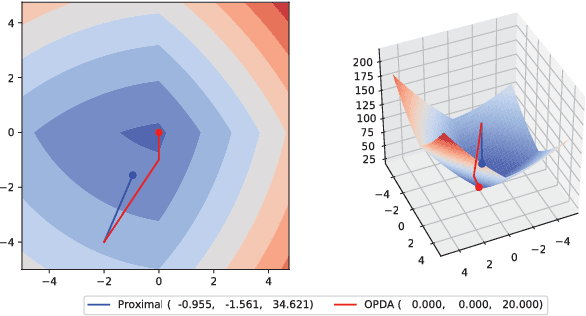
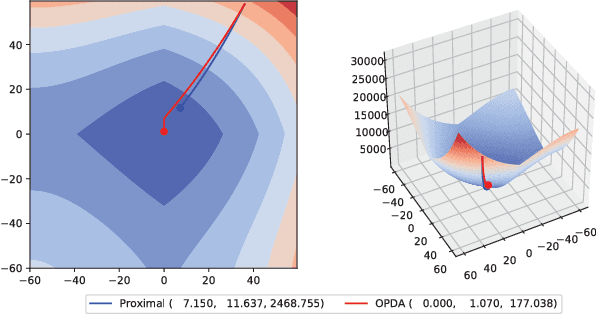
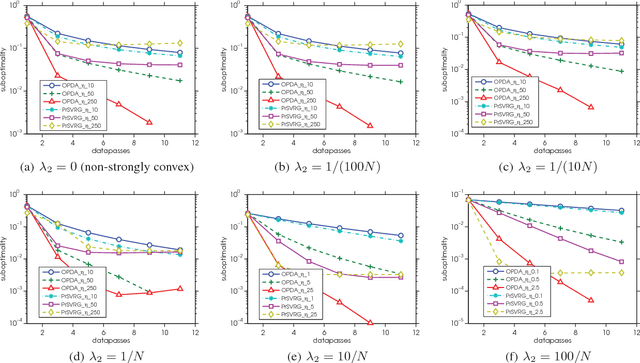
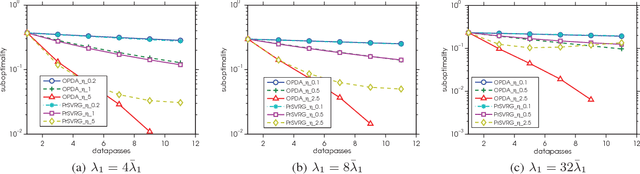
The $L_1$-regularized models are widely used for sparse regression or classification tasks. In this paper, we propose the orthant-wise passive descent algorithm (OPDA) for optimizing $L_1$-regularized models, as an improved substitute of proximal algorithms, which are the standard tools for optimizing the models nowadays. OPDA uses a stochastic variance-reduced gradient (SVRG) to initialize the descent direction, then apply a novel alignment operator to encourage each element keeping the same sign after one iteration of update, so the parameter remains in the same orthant as before. It also explicitly suppresses the magnitude of each element to impose sparsity. The quasi-Newton update can be utilized to incorporate curvature information and accelerate the speed. We prove a linear convergence rate for OPDA on general smooth and strongly-convex loss functions. By conducting experiments on $L_1$-regularized logistic regression and convolutional neural networks, we show that OPDA outperforms state-of-the-art stochastic proximal algorithms, implying a wide range of applications in training sparse models.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge