Tools for Mathematical Ludology
Paper and Code
Jan 06, 2020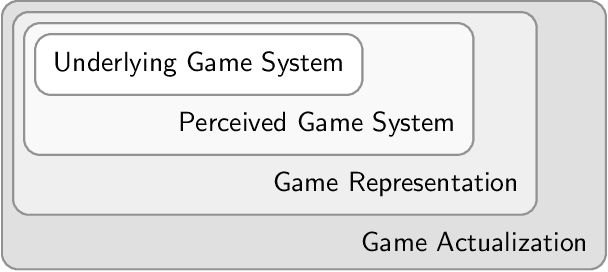
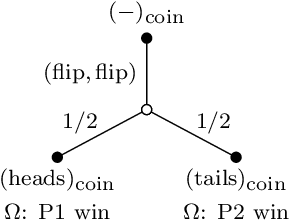
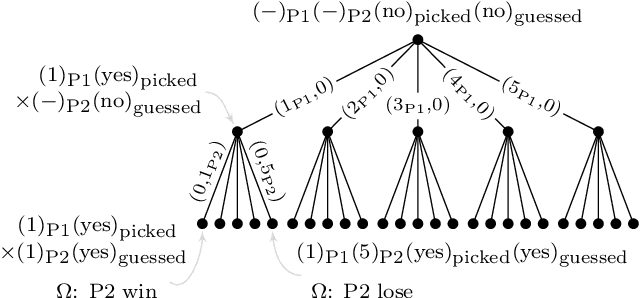
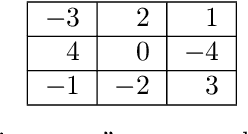
We propose the study of mathematical ludology, which aims to formally interrogate questions of interest to game studies and game design in particular. The goal is to extend our mathematical understanding of complex games beyond decision-making---the typical focus of game theory and artificial intelligence efforts---to explore other aspects such as game mechanics, structure, relationships between games, and connections between game rules and user-interfaces, as well as exploring related gameplay phenomena and typical player behavior. In this paper, we build a basic foundation for this line of study by developing a hierarchy of game descriptions, mathematical formalism to compactly describe complex discrete games, and equivalence relations on the space of game systems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge