Time and the Prisoner's Dilemma
Paper and Code
Jan 22, 2007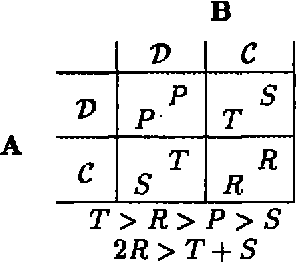
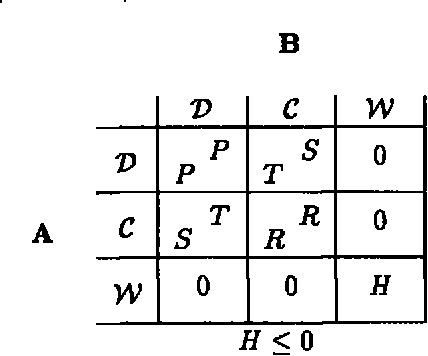
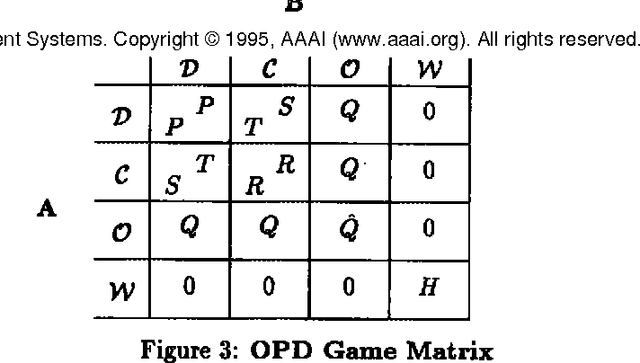
This paper examines the integration of computational complexity into game theoretic models. The example focused on is the Prisoner's Dilemma, repeated for a finite length of time. We show that a minimal bound on the players' computational ability is sufficient to enable cooperative behavior. In addition, a variant of the repeated Prisoner's Dilemma game is suggested, in which players have the choice of opting out. This modification enriches the game and suggests dominance of cooperative strategies. Competitive analysis is suggested as a tool for investigating sub-optimal (but computationally tractable) strategies and game theoretic models in general. Using competitive analysis, it is shown that for bounded players, a sub-optimal strategy might be the optimal choice, given resource limitations.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge