The Ramanujan Library -- Automated Discovery on the Hypergraph of Integer Relations
Paper and Code
Dec 16, 2024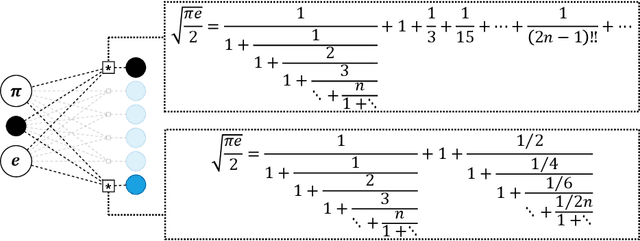
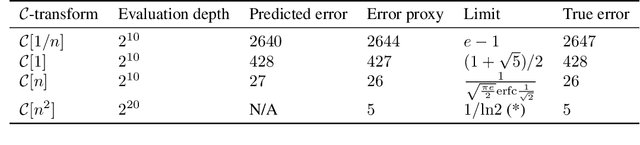
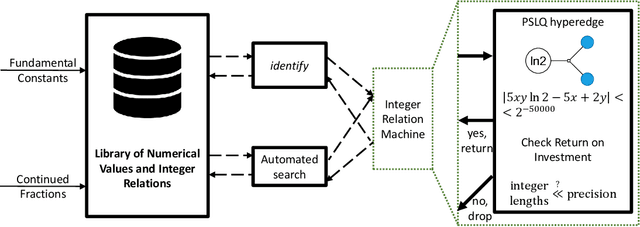
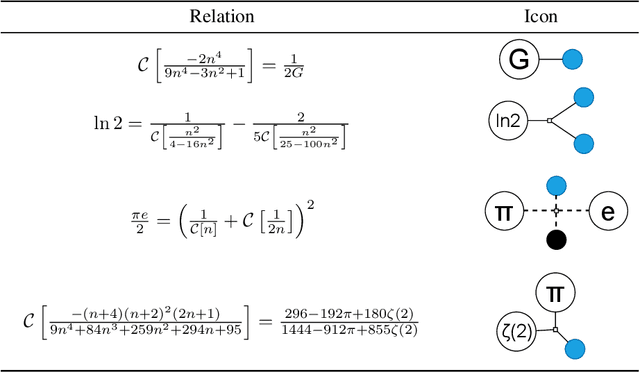
Fundamental mathematical constants appear in nearly every field of science, from physics to biology. Formulas that connect different constants often bring great insight by hinting at connections between previously disparate fields. Discoveries of such relations, however, have remained scarce events, relying on sporadic strokes of creativity by human mathematicians. Recent developments of algorithms for automated conjecture generation have accelerated the discovery of formulas for specific constants. Yet, the discovery of connections between constants has not been addressed. In this paper, we present the first library dedicated to mathematical constants and their interrelations. This library can serve as a central repository of knowledge for scientists from different areas, and as a collaborative platform for development of new algorithms. The library is based on a new representation that we propose for organizing the formulas of mathematical constants: a hypergraph, with each node representing a constant and each edge representing a formula. Using this representation, we propose and demonstrate a systematic approach for automatically enriching this library using PSLQ, an integer relation algorithm based on QR decomposition and lattice construction. During its development and testing, our strategy led to the discovery of 75 previously unknown connections between constants, including a new formula for the `first continued fraction' constant $C_1$, novel formulas for natural logarithms, and new formulas connecting $\pi$ and $e$. The latter formulas generalize a century-old relation between $\pi$ and $e$ by Ramanujan, which until now was considered a singular formula and is now found to be part of a broader mathematical structure. The code supporting this library is a public, open-source API that can serve researchers in experimental mathematics and other fields of science.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge