The Mechanism of Prediction Head in Non-contrastive Self-supervised Learning
Paper and Code
May 14, 2022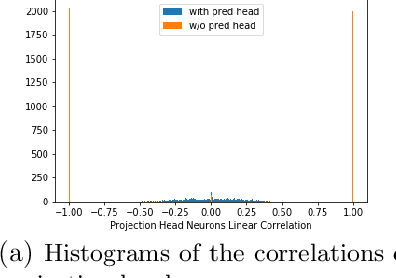
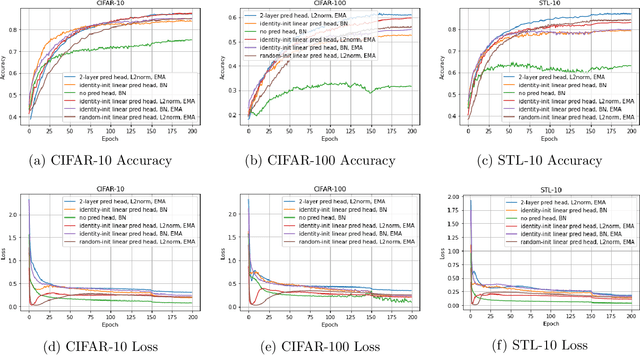
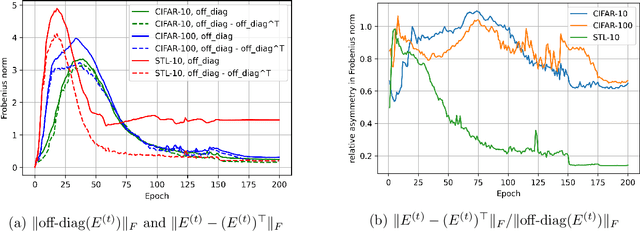
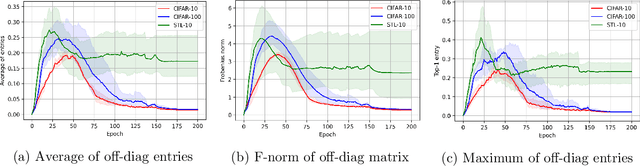
Recently the surprising discovery of the Bootstrap Your Own Latent (BYOL) method by Grill et al. shows the negative term in contrastive loss can be removed if we add the so-called prediction head to the network. This initiated the research of non-contrastive self-supervised learning. It is mysterious why even when there exist trivial collapsed global optimal solutions, neural networks trained by (stochastic) gradient descent can still learn competitive representations. This phenomenon is a typical example of implicit bias in deep learning and remains little understood. In this work, we present our empirical and theoretical discoveries on non-contrastive self-supervised learning. Empirically, we find that when the prediction head is initialized as an identity matrix with only its off-diagonal entries being trainable, the network can learn competitive representations even though the trivial optima still exist in the training objective. Theoretically, we present a framework to understand the behavior of the trainable, but identity-initialized prediction head. Under a simple setting, we characterized the substitution effect and acceleration effect of the prediction head. The substitution effect happens when learning the stronger features in some neurons can substitute for learning these features in other neurons through updating the prediction head. And the acceleration effect happens when the substituted features can accelerate the learning of other weaker features to prevent them from being ignored. These two effects enable the neural networks to learn all the features rather than focus only on learning the stronger features, which is likely the cause of the dimensional collapse phenomenon. To the best of our knowledge, this is also the first end-to-end optimization guarantee for non-contrastive methods using nonlinear neural networks with a trainable prediction head and normalization.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge