The Effects of Perfect and Sample Information on Fuzzy Utilities in Decision-Making
Paper and Code
Mar 27, 2013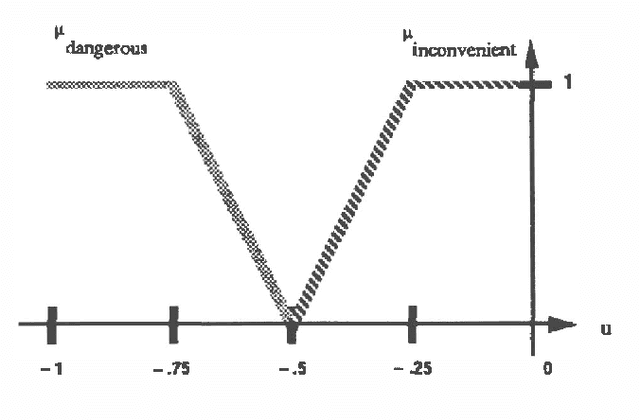
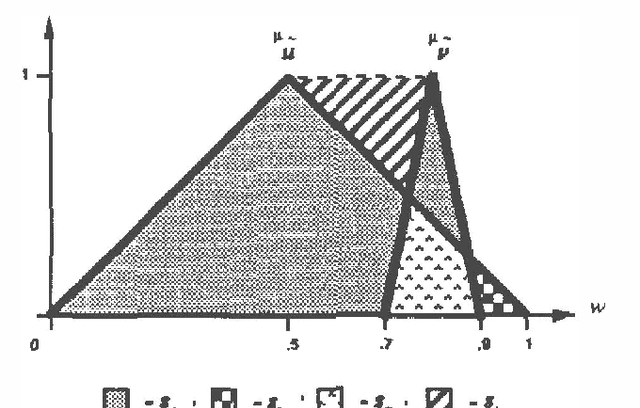
In this paper, we first consider a Bayesian framework and model the "utility function" in terms of fuzzy random variables. On the basis of this model, we define the "prior (fuzzy) expected utility" associated with each action, and the corresponding "posterior (fuzzy) expected utility given sample information from a random experiment". The aim of this paper is to analyze how sample information can affect the expected utility. In this way, by using some fuzzy preference relations, we conclude that sample information allows a decision maker to increase the expected utility on the average. The upper bound on the value of the expected utility is when the decision maker has perfect information. Applications of this work to the field of artificial intelligence are presented through two examples.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge