The covariance matrix of Green's functions and its application to machine learning
Paper and Code
Apr 14, 2020
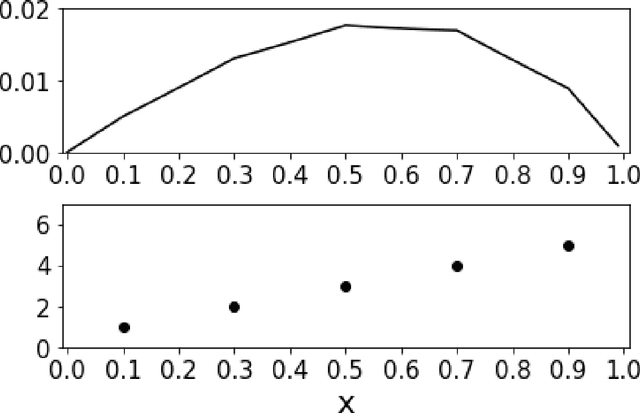
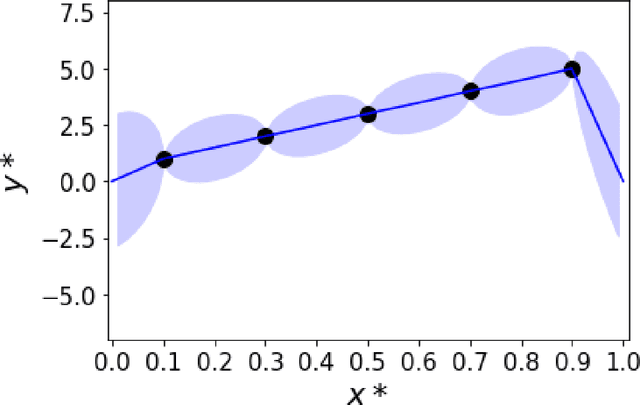
In this paper, a regression algorithm based on Green's function theory is proposed and implemented. We first survey Green's function for the Dirichlet boundary value problem of 2nd order linear ordinary differential equation, which is a reproducing kernel of a suitable Hilbert space. We next consider a covariance matrix composed of the normalized Green's function, which is regarded as aprobability density function. By supporting Bayesian approach, the covariance matrix gives predictive distribution, which has the predictive mean $\mu$ and the confidence interval [$\mu$-2s, $\mu$+2s], where s stands for a standard deviation.
* 9 pages, 6 figures
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge