Technical Report of "Deductive Joint Support for Rational Unrestricted Rebuttal"
Paper and Code
May 07, 2020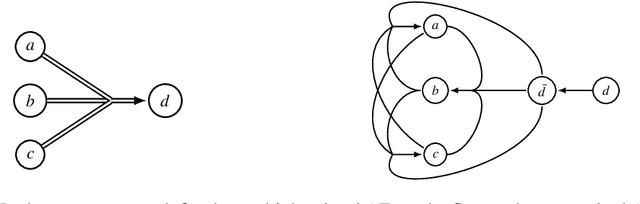
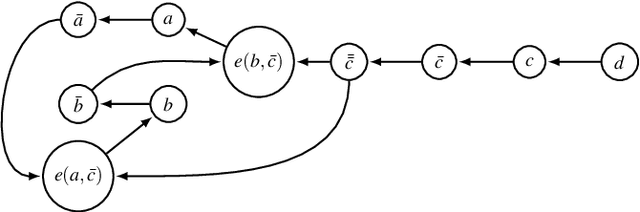
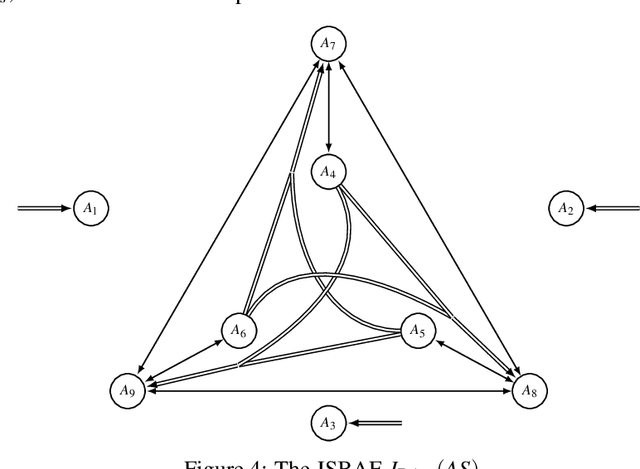
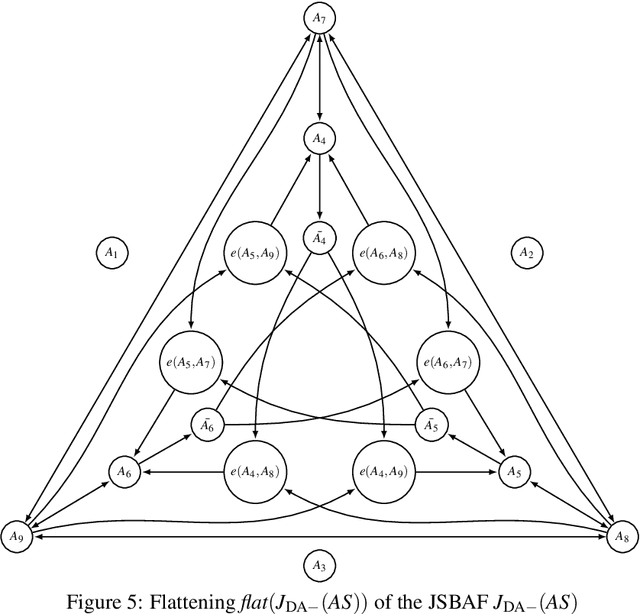
In ASPIC-style structured argumentation an argument can rebut another argument by attacking its conclusion. Two ways of formalizing rebuttal have been proposed: In restricted rebuttal, the attacked conclusion must have been arrived at with a defeasible rule, whereas in unrestricted rebuttal, it may have been arrived at with a strict rule, as long as at least one of the antecedents of this strict rule was already defeasible. One systematic way of choosing between various possible definitions of a framework for structured argumentation is to study what rationality postulates are satisfied by which definition, for example whether the closure postulate holds, i.e. whether the accepted conclusions are closed under strict rules. While having some benefits, the proposal to use unrestricted rebuttal faces the problem that the closure postulate only holds for the grounded semantics but fails when other argumentation semantics are applied, whereas with restricted rebuttal the closure postulate always holds. In this paper we propose that ASPIC-style argumentation can benefit from keeping track not only of the attack relation between arguments, but also the relation of deductive joint support that holds between a set of arguments and an argument that was constructed from that set using a strict rule. By taking this deductive joint support relation into account while determining the extensions, the closure postulate holds with unrestricted rebuttal under all admissibility-based semantics. We define the semantics of deductive joint support through the flattening method.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge