Symbolic Neutrosophic Theory
Paper and Code
Oct 18, 2015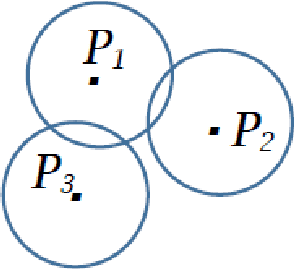
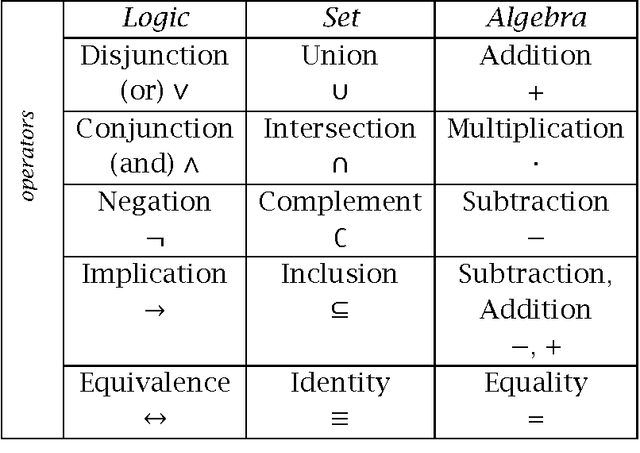
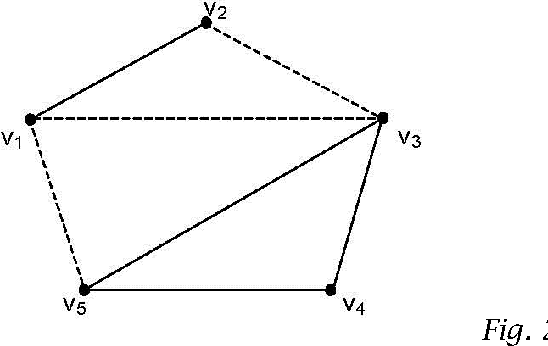
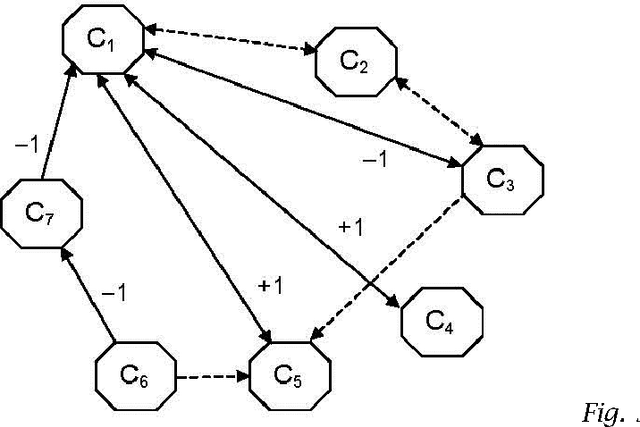
Symbolic (or Literal) Neutrosophic Theory is referring to the use of abstract symbols (i.e. the letters T, I, F, or their refined indexed letters Tj, Ik, Fl) in neutrosophics. We extend the dialectical triad thesis-antithesis-synthesis to the neutrosophic tetrad thesis-antithesis-neutrothesis-neutrosynthesis. The we introduce the neutrosophic system that is a quasi or (t,i,f) classical system, in the sense that the neutrosophic system deals with quasi-terms (concepts, attributes, etc.). Then the notions of Neutrosophic Axiom, Neutrosophic Deducibility, Degree of Contradiction (Dissimilarity) of Two Neutrosophic Axioms, etc. Afterwards a new type of structures, called (t, i, f) Neutrosophic Structures, and we show particular cases of such structures in geometry and in algebra. Also, a short history of the neutrosophic set, neutrosophic numerical components and neutrosophic literal components, neutrosophic numbers, etc. We construct examples of splitting the literal indeterminacy (I) into literal subindeterminacies (I1, I2, and so on, Ir), and to define a multiplication law of these literal subindeterminacies in order to be able to build refined I neutrosophic algebraic structures. We define three neutrosophic actions and their properties. We then introduce the prevalence order on T,I,F with respect to a given neutrosophic operator. And the refinement of neutrosophic entities A, neutA, and antiA. Then we extend the classical logical operators to neutrosophic literal (symbolic) logical operators and to refined literal (symbolic) logical operators, and we define the refinement neutrosophic literal (symbolic) space. We introduce the neutrosophic quadruple numbers (a+bT+cI+dF) and the refined neutrosophic quadruple numbers. Then we define an absorbance law, based on a prevalence order, in order to multiply the neutrosophic quadruple numbers.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge