Supervised learning with generalized tensor networks

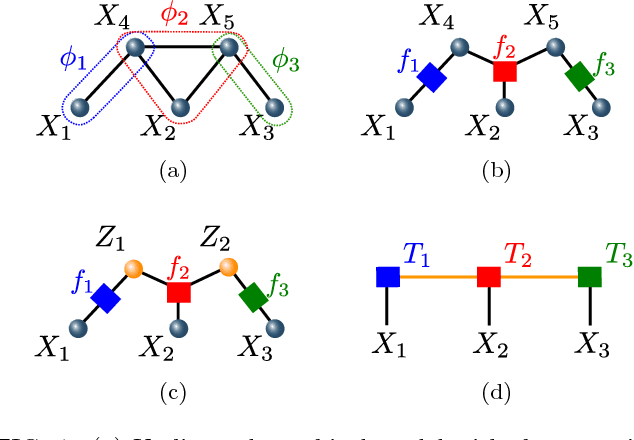
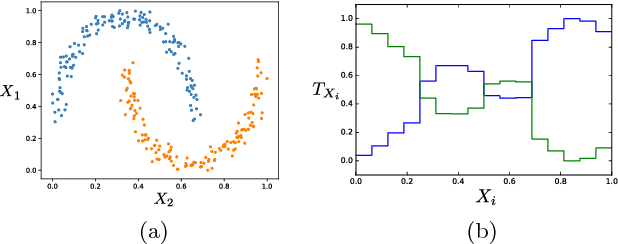
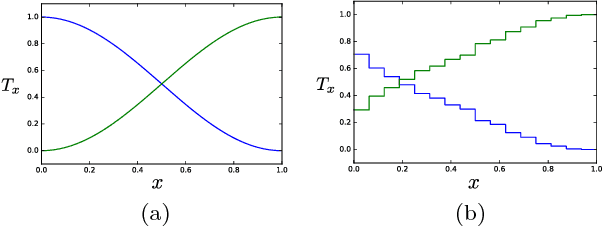
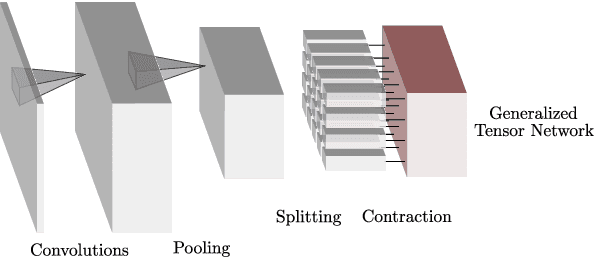
Tensor networks have found a wide use in a variety of applications in physics and computer science, recently leading to both theoretical insights as well as practical algorithms in machine learning. In this work we explore the connection between tensor networks and probabilistic graphical models, and show that it motivates the definition of generalized tensor networks where information from a tensor can be copied and reused in other parts of the network. We discuss the relationship between generalized tensor network architectures used in quantum physics, such as String-Bond States and Entangled Plaquette States, and architectures commonly used in machine learning. We provide an algorithm to train these networks in a supervised learning context and show that they overcome the limitations of regular tensor networks in higher dimensions, while keeping the computation efficient. A method to combine neural networks and tensor networks as part of a common deep learning architecture is also introduced. We benchmark our algorithm for several generalized tensor network architectures on the task of classifying images and sounds, and show that they outperform previously introduced tensor network algorithms. Some of the models we consider can be realized on a quantum computer and may guide the development of near-term quantum machine learning architectures.