Stochastic Sensitivity Analysis Using Fuzzy Influence Diagrams
Paper and Code
Mar 27, 2013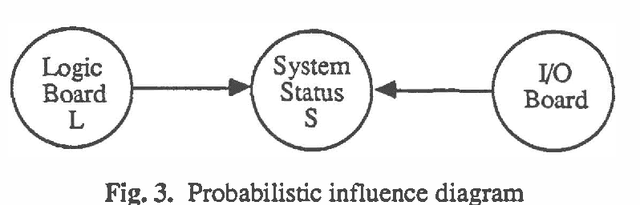
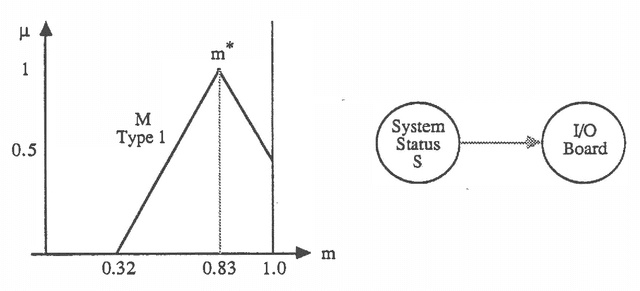
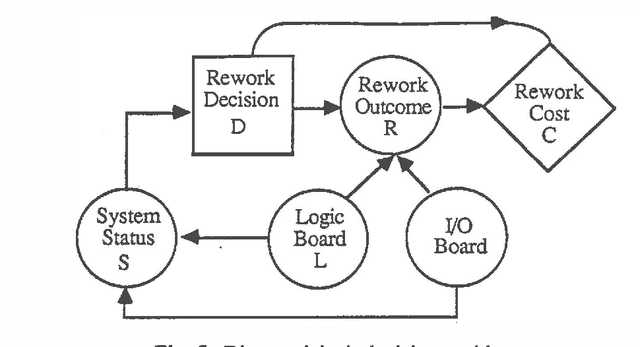
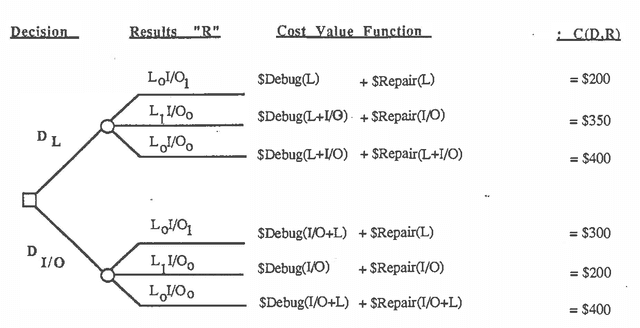
The practice of stochastic sensitivity analysis described in the decision analysis literature is a testimonial to the need for considering deviations from precise point estimates of uncertainty. We propose the use of Bayesian fuzzy probabilities within an influence diagram computational scheme for performing sensitivity analysis during the solution of probabilistic inference and decision problems. Unlike other parametric approaches, the proposed scheme does not require resolving the problem for the varying probability point estimates. We claim that the solution to fuzzy influence diagrams provides as much information as the classical point estimate approach plus additional information concerning stochastic sensitivity. An example based on diagnostic decision making in microcomputer assembly is used to illustrate this idea. We claim that the solution to fuzzy influence diagrams provides as much information as the classical point estimate approach plus additional interval information that is useful for stochastic sensitivity analysis.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge