Statistical Theory for Imbalanced Binary Classification
Paper and Code
Jul 05, 2021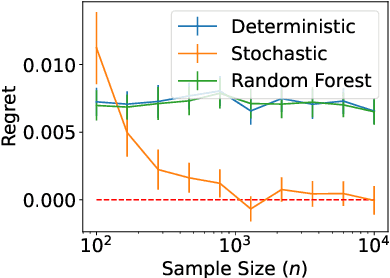
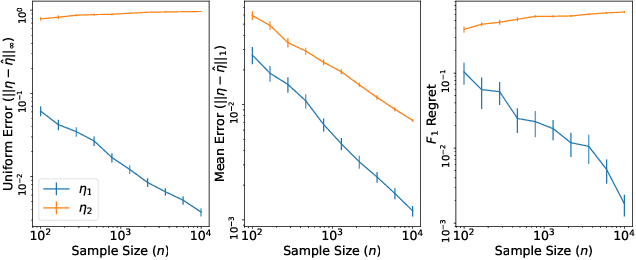
Within the vast body of statistical theory developed for binary classification, few meaningful results exist for imbalanced classification, in which data are dominated by samples from one of the two classes. Existing theory faces at least two main challenges. First, meaningful results must consider more complex performance measures than classification accuracy. To address this, we characterize a novel generalization of the Bayes-optimal classifier to any performance metric computed from the confusion matrix, and we use this to show how relative performance guarantees can be obtained in terms of the error of estimating the class probability function under uniform ($\mathcal{L}_\infty$) loss. Second, as we show, optimal classification performance depends on certain properties of class imbalance that have not previously been formalized. Specifically, we propose a novel sub-type of class imbalance, which we call Uniform Class Imbalance. We analyze how Uniform Class Imbalance influences optimal classifier performance and show that it necessitates different classifier behavior than other types of class imbalance. We further illustrate these two contributions in the case of $k$-nearest neighbor classification, for which we develop novel guarantees. Together, these results provide some of the first meaningful finite-sample statistical theory for imbalanced binary classification.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge