Sparse Estimation with Generalized Beta Mixture and the Horseshoe Prior
Paper and Code
Nov 10, 2014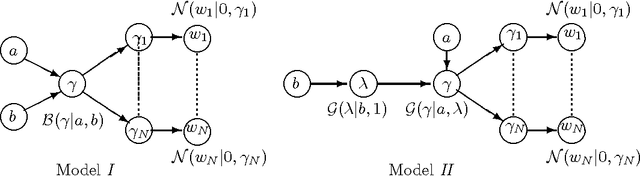
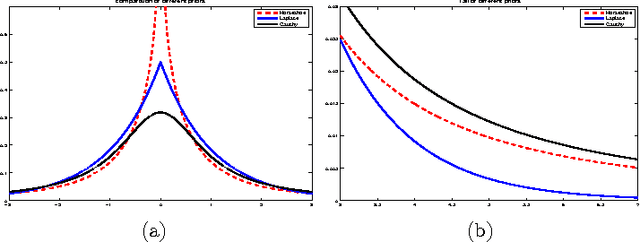
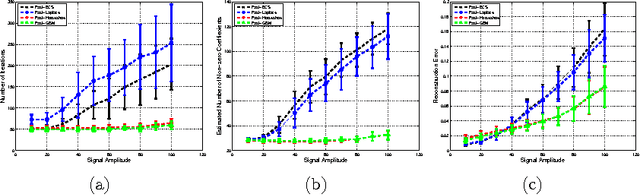
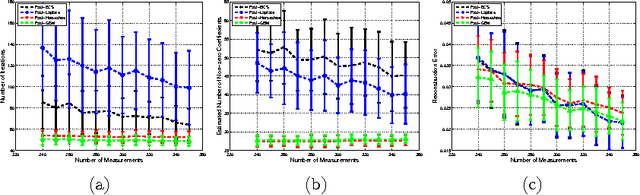
In this paper, the use of the Generalized Beta Mixture (GBM) and Horseshoe distributions as priors in the Bayesian Compressive Sensing framework is proposed. The distributions are considered in a two-layer hierarchical model, making the corresponding inference problem amenable to Expectation Maximization (EM). We present an explicit, algebraic EM-update rule for the models, yielding two fast and experimentally validated algorithms for signal recovery. Experimental results show that our algorithms outperform state-of-the-art methods on a wide range of sparsity levels and amplitudes in terms of reconstruction accuracy, convergence rate and sparsity. The largest improvement can be observed for sparse signals with high amplitudes.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge