Solving Tree Problems with Category Theory
Paper and Code
Oct 16, 2018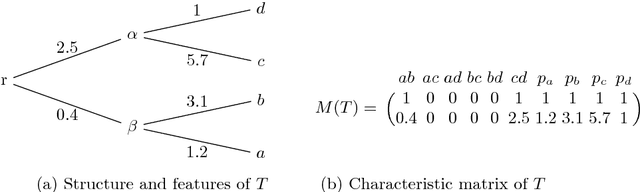
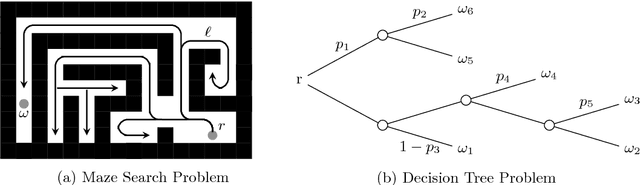
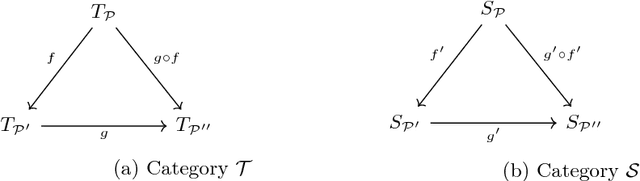
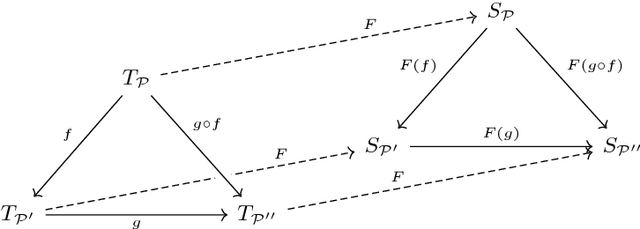
Artificial Intelligence (AI) has long pursued models, theories, and techniques to imbue machines with human-like general intelligence. Yet even the currently predominant data-driven approaches in AI seem to be lacking humans' unique ability to solve wide ranges of problems. This situation begs the question of the existence of principles that underlie general problem-solving capabilities. We approach this question through the mathematical formulation of analogies across different problems and solutions. We focus in particular on problems that could be represented as tree-like structures. Most importantly, we adopt a category-theoretic approach in formalising tree problems as categories, and in proving the existence of equivalences across apparently unrelated problem domains. We prove the existence of a functor between the category of tree problems and the category of solutions. We also provide a weaker version of the functor by quantifying equivalences of problem categories using a metric on tree problems.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge