Set Interdependence Transformer: Set-to-Sequence Neural Networks for Permutation Learning and Structure Prediction
Paper and Code
Jun 08, 2022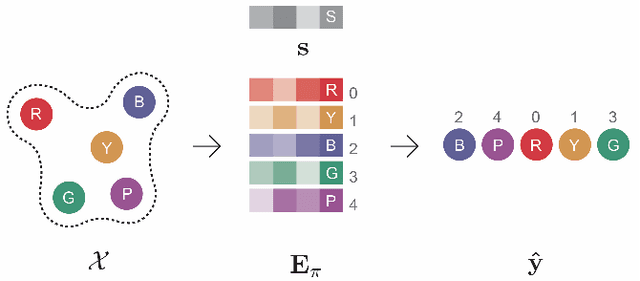
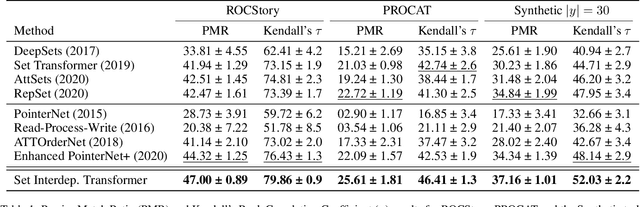
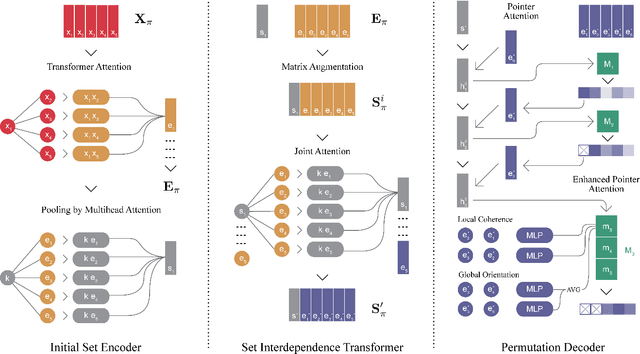
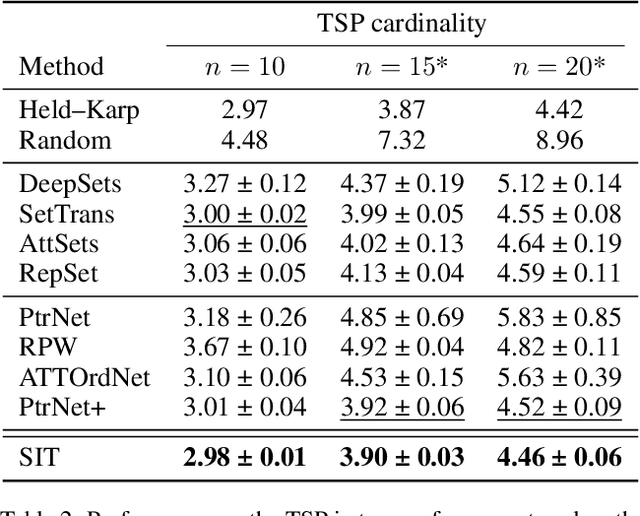
The task of learning to map an input set onto a permuted sequence of its elements is challenging for neural networks. Set-to-sequence problems occur in natural language processing, computer vision and structure prediction, where interactions between elements of large sets define the optimal output. Models must exhibit relational reasoning, handle varying cardinalities and manage combinatorial complexity. Previous attention-based methods require $n$ layers of their set transformations to explicitly represent $n$-th order relations. Our aim is to enhance their ability to efficiently model higher-order interactions through an additional interdependence component. We propose a novel neural set encoding method called the Set Interdependence Transformer, capable of relating the set's permutation invariant representation to its elements within sets of any cardinality. We combine it with a permutation learning module into a complete, 3-part set-to-sequence model and demonstrate its state-of-the-art performance on a number of tasks. These range from combinatorial optimization problems, through permutation learning challenges on both synthetic and established NLP datasets for sentence ordering, to a novel domain of product catalog structure prediction. Additionally, the network's ability to generalize to unseen sequence lengths is investigated and a comparative empirical analysis of the existing methods' ability to learn higher-order interactions is provided.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge