Second-Order Perturbation Theory-Based Digital Predistortion for Fiber Nonlinearity Compensation
Paper and Code
Jun 27, 2021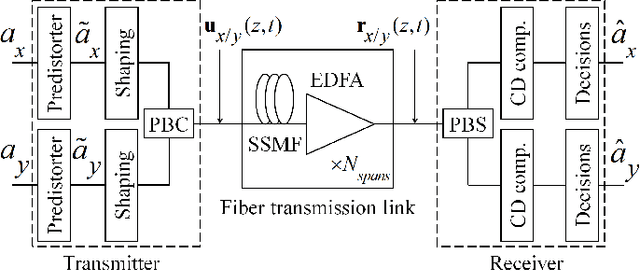
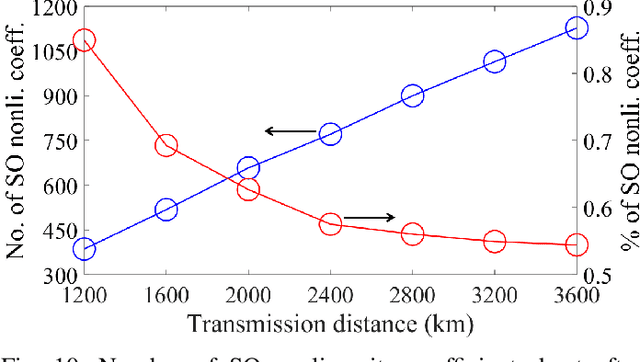
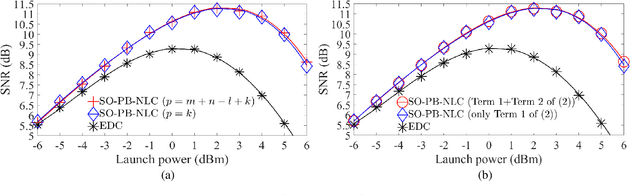
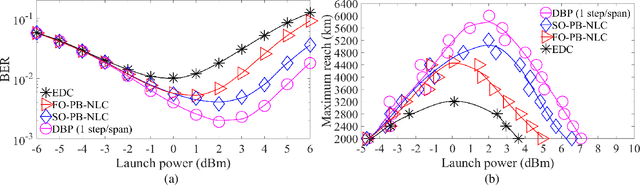
The first-order (FO) perturbation theory-based nonlinearity compensation (PB-NLC) technique has been widely investigated to combat the detrimental effects of the intra-channel Kerr nonlinearity in polarization-multiplexed (Pol-Mux) optical fiber communication systems. However, the NLC performance of the FO-PB-NLC technique is significantly limited in highly nonlinear regimes of the Pol-Mux long-haul optical transmission systems. In this paper, we extend the FO theory to second-order (SO) to improve the NLC performance. This technique is referred to as the SO-PB-NLC. A detailed theoretical analysis is performed to derive the SO perturbative field for a Pol-Mux optical transmission system. Following that, we investigate a few simplifying assumptions to reduce the implementation complexity of the SO-PB-NLC technique. The numerical simulations for a single-channel system show that the SO-PB-NLC technique provides an improved bit-error-rate performance and increases the transmission reach, in comparison with the FO-PB-NLC technique. The complexity analysis demonstrates that the proposed SO-PB-NLC technique has a reduced computational complexity when compared to the digital back-propagation with one step per span.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge