Robustness of Neural Networks to Parameter Quantization
Paper and Code
Mar 26, 2019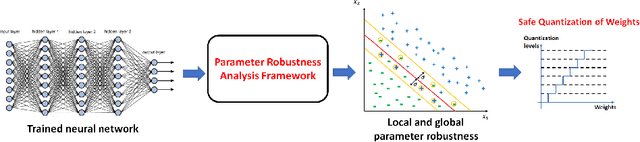
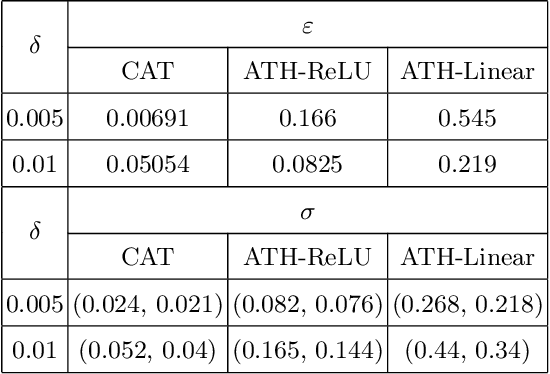

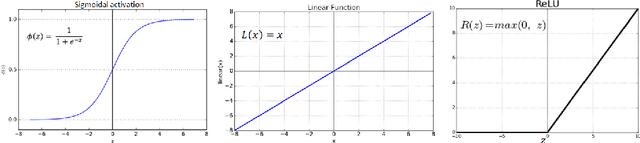
Quantization, a commonly used technique to reduce the memory footprint of a neural network for edge computing, entails reducing the precision of the floating-point representation used for the parameters of the network. The impact of such rounding-off errors on the overall performance of the neural network is estimated using testing, which is not exhaustive and thus cannot be used to guarantee the safety of the model. We present a framework based on Satisfiability Modulo Theory (SMT) solvers to quantify the robustness of neural networks to parameter perturbation. To this end, we introduce notions of local and global robustness that capture the deviation in the confidence of class assignments due to parameter quantization. The robustness notions are then cast as instances of SMT problems and solved automatically using solvers, such as dReal. We demonstrate our framework on two simple Multi-Layer Perceptrons (MLP) that perform binary classification on a two-dimensional input. In addition to quantifying the robustness, we also show that Rectified Linear Unit activation results in higher robustness than linear activations for our MLPs.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge