Robust Phase Retrieval via Reverse Kullback-Leibler Divergence and Wirtinger Flow
Paper and Code
Apr 20, 2022
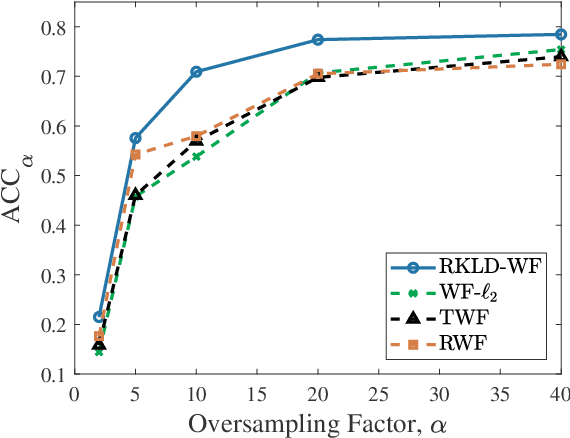
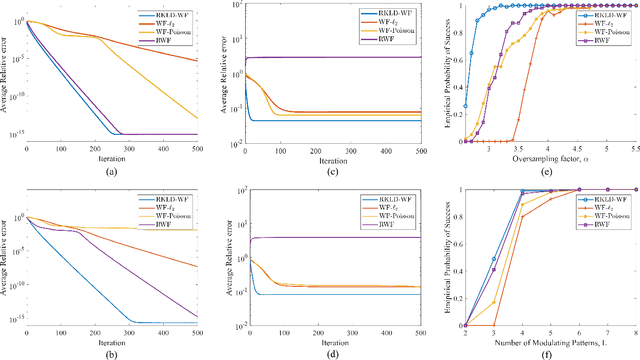
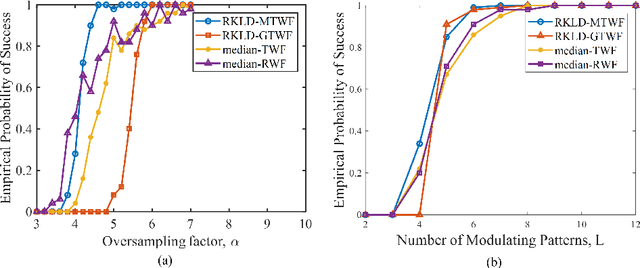
Robustness to noise and outliers is a desirable trait in phase retrieval algorithms for many applications in imaging and signal processing. In this paper, we develop a novel robust phase retrieval algorithm based on the minimization of reverse Kullback-Leibler divergence (RKLD) within the Wirtinger Flow (WF) framework. We use RKLD over intensity-only measurements in two distinct ways: i) to design a novel initial estimate based on minimum distortion design of spectral estimates, and ii) as a loss function for iterative refinement based on WF. The RKLD-based loss function offers implicit regularization by processing data at the logarithmic scale and provides the following benefits: suppressing the influence of large magnitude errors and promoting projections orthogonal to noise subspace. We present three algorithms based on RKLD minimization, including two with truncation schemes to enhance the robustness to significant contamination. Our numerical study demonstrates the advantages of our algorithms in terms of sample efficiency, convergence speed, and robustness to outliers over the state-of-the-art techniques using both synthetic and real optical imaging data.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge