Risk averse non-stationary multi-armed bandits
Paper and Code
Sep 28, 2021
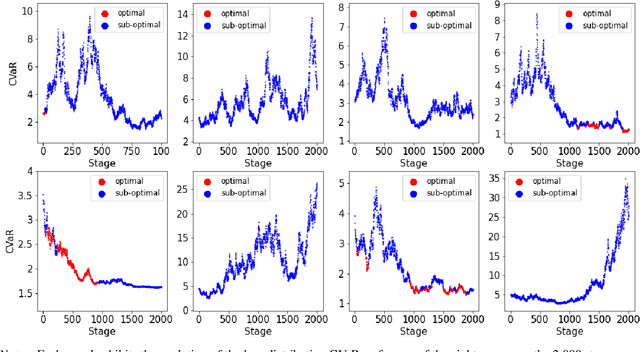
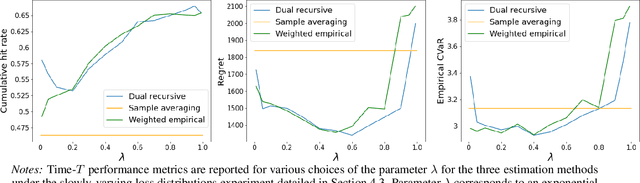
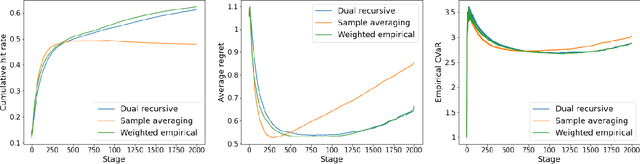
This paper tackles the risk averse multi-armed bandits problem when incurred losses are non-stationary. The conditional value-at-risk (CVaR) is used as the objective function. Two estimation methods are proposed for this objective function in the presence of non-stationary losses, one relying on a weighted empirical distribution of losses and another on the dual representation of the CVaR. Such estimates can then be embedded into classic arm selection methods such as epsilon-greedy policies. Simulation experiments assess the performance of the arm selection algorithms based on the two novel estimation approaches, and such policies are shown to outperform naive benchmarks not taking non-stationarity into account.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge