RIS Design to Optimize the CRB for Source Localization
Paper and Code
Oct 01, 2022
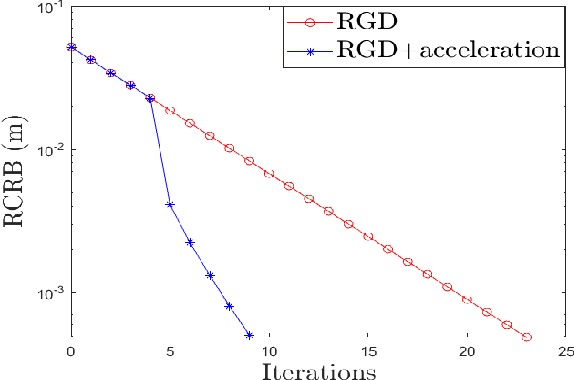
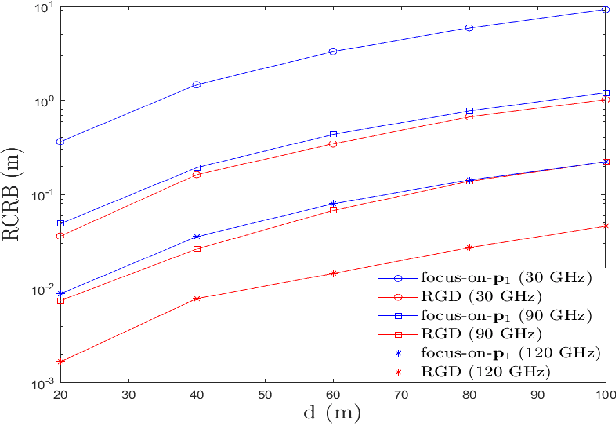

Reconfigurable Intelligent Surface (RIS) plays a pivotal role in enhancing source localization accuracy. Based on the information inequality of Fisher information analyses, the Cram\'{e}r-Rao Bound (CRB) of the localization error can be used to evaluate the localization accuracy for a given set of RIS coefficients. However, there is a lack of research in optimizing these RIS coefficients to decrease the CRB under the constraint imposed by the RIS hardware. In this paper, we adopt the manifold optimization method to derive the locally optimal CRB of the localization error, where the RIS coefficients are restricted to lie on the complex circle manifold. Specifically, the Wirtinger derivatives are calculated in the gradient descent part, and the Riemannian nonlinear acceleration technique is employed to speed up the convergence rate. Simulation results show that the proposed method can yield the locally optimal RIS coefficients and can significantly decrease the CRB of localization error. Moreover, the iteration number can be reduced by the acceleration technique.
 Add to Chrome
Add to Chrome Add to Firefox
Add to Firefox Add to Edge
Add to Edge